Что самое главное в характеристиках звуковой аппаратуры? Мощность, диапазон воспроизводимых частот или уровни звукового давления — на что смотреть? На амплитудно-частотную характеристику (АЧХ), именно она может показать, как работает то или иное аудиооборудование. АЧХ – это то, на что вы должны обращать внимание в первую очередь при выборе устройств, другие характеристики теряют всякую ценность при плохой АЧХ. Амплитудно-частотная характеристика показывает зависимость отклонения в громкости воспроизводимого звука в (дБ) от его частоты в (Гц).
Человеческий слух способен воспринимать звуковые волны частотой от 20 Гц до 20 000 Гц. Это в идеале. На самом деле, данный частотный диапазон сужается с возрастом (особенно высокие частоты) и его рамки зависят от пола и гигиены слуха. Например, любители громкой музыки, наушников и работники шумных производств частично теряют слух, и верхняя граница слышимого диапазона сильно смещается. Поэтому еще раз призываем вас беречь свой слух и не забывать о его гигиене. Подробнее об этом можно почитать здесь.
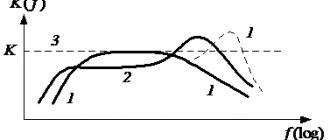
Что значит хорошая АЧХ?
Если ограничиться одним предложением, что АЧХ должна иметь форму, близкую к прямой. Но мы не ограничимся, конечно, а расскажем поподробнее.
Если устройство имеет хорошую АЧХ, то оно правильно воспроизводит все низкие, средние и высокие частоты в правильном соотношении между собой, что обеспечивает чистый, богатый и насыщенный звук. По АЧХ можно увидеть, на сколько дБ звук отклоняется от нормы в конкретном диапазоне частот. Ориентируемся на следующие цифры:
- ± 1 дБ – минимально различимое изменение звукового давления;
- ± 3 дБ – заметное, но допустимое отклонение;
- > 10 дБ – существенное отклонение в громкости, могут неприятные ощущения при прослушивании.
Напомним, что шкала громкости, выраженной в децибелах (дБ) является логарифмической, поэтому увеличение громкости на 10 дБ означает, что звук будет звучать в два раза громче. О характеристиках звука можно почитать здесь. Неравномерность АЧХ должна быть указана производителем, иначе стоит настороженно относиться к данному продукту. Таким образом, частотный диапазон, в пределах которого качество звука соответствует заявленному, отмечается с помощью крайних точек (например, 40 Гц – 16000 Гц), вне этого диапазона наблюдается значительное отклонение от усредненных данных, причем величина отклонения должна быть также указана (например ± 1дБ или ± 3 дБ). Например, в описании акустической системы может быть написано: 50 Гц – 20 кГц (± 3 дБ). Следовательно, стоит понимать эту запись так: данная акустическая система имеет достоверное звучание в диапазоне 50 Гц – 20 кГц и имеет отклонения от линейности в районе трёх децибел в обе стороны, а за рамками этих границ резко увеличивается неравномерность звучания. На самом деле, и такая запись не является особо информативной и поводом доверять производителю, т.к. АЧХ нужно показать в виде графика. Обнаружили вы график АЧХ и… что дальше? Как его читать и понимать?
Гармонические и негармонические сигналы.
И для начала чуть подробнее разберемся, как классифицируются сигналы. В первую очередь, нас интересуют периодические сигналы. Их форма повторяется через определенный интервал времени T, называемый периодом. Периодические сигналы в свою очередь делятся на два больших класса — гармонические и негармонические. Гармонический сигнал — это сигнал, который можно описать следующей функцией:
y = A cos(wt + \phi)
Здесь A — амплитуда сигнала, w — циклическая частота, а \phi — начальная фаза. Может возникнуть логичный вопрос — разве синусоидальный сигнал не является гармоническим? Конечно, является, дело в том, что sin\alpha = cos(\frac{\pi}{2}\medspace-\medspace \alpha) — то есть сигналы отличаются начальной фазой, соответственно, синусоидальный сигнал не противоречит определению, которое мы дали для гармонических колебаний.
Вторым подклассом периодических сигналов являются негармонические колебания. Вот пример негармонического сигнала:
Как видите, несмотря на свой вид, сигнал остается периодическим, то есть его форма повторяется через интервал времени, равный периоду.
Для работы с такими сигналами и их исследования существует определенная методика, которая заключается в разложении сигнала в ряд Фурье. Суть состоит в том, что негармонический периодический сигнал (при выполнении определенных условий) можно представить в виде суммы гармонических колебаний с определенными амплитудами, частотами и начальными фазами. Важным нюансом является то, что все гармонические колебания, которые участвуют в суммировании, должны иметь частоты, кратные частоте исходного негармонического сигнала. Возможно это пока не совсем понятно, так что рассмотрим практический пример и разберемся подробнее. И для примера используем сигнал, который изображен на рисунке чуть выше. Его можно представить следующим образом:
u(t) = u_1(t) + u_2(t) = 2 sin(t) + 1.5 sin(2t)
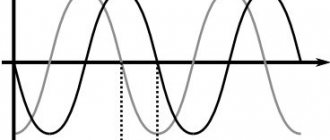
Давайте изобразим все эти сигналы на одном графике:
Функции u_1(t), u_2(t) называют гармониками сигнала, а ту из них, период которой равен периоду негармонического сигнала, называют первой или основной гармоникой. В данном случае первой гармоникой является функция u_1(t) (ее частота равна частоте исследуемого негармонического сигнала, соответственно, равны и их периоды). А функция u_2(t) = 1.5 sin(2t) представляет из себя ни что иное как вторую гармонику сигнала (ее частота в два раза больше). В общем случае, негармонический сигнал раскладывается на бесконечное число гармоник:
u(t) = U_0 + \sum_{i=0}^{\infty}{U_{k}\thinspace sin(\thinspace kwt + \phi_k\thinspace )}
Здесь U_k — амплитуда, а \phi_k — начальная фаза k-ой гармоники. Как мы уже упомянули чуть ранее, частоты всех гармоник кратны частоте первой гармоники, собственно, это мы и наблюдаем в данной формуле. U_0 — это нулевая гармоника, ее частота равна 0, она равна среднему значению функции за период. Почему среднему? Смотрите — среднее значения функции синуса за период равно 0, а значит при усреднении в этой формуле все слагаемые, кроме U_0 будут равны 0