Временная область и частотная область
Когда вы смотрите на электрический сигнал на осциллографе, вы видите линию, которая представляет изменения напряжения относительно времени. В любой конкретный момент времени сигнал имеет только одно значение напряжения. На осциллографе вы видите представление сигнала во временной области.
Типовая осциллограмма проста и интуитивно понятна, но она также имеет некоторые ограничения, поскольку она напрямую не раскрывает частотный состав сигнала. В отличие от представления во временной области, в котором один момент времени соответствует только одному значению напряжения, представление в частотной области (также называемое спектром) передает информацию о сигнале посредством определения различных частотных компонентов, которые представлены одновременно.
Рисунок 1 – Представления во временной области синусоидального (вверху) и прямоугольного (внизу) сигналов
Рисунок 2 – Частотные представления синусоидального (вверху) и прямоугольного (внизу) сигналов
▍ Общий алгоритм построения
Существует несколько подходов к проектированию КИХ-фильтров, из которых наиболее простым и интуитивно-понятным является следующий:
- В частотном домене задаётся желаемая АЧХ фильтра;
- Производится обратное преобразование Фурье:
- Накладывается оконная функция.
Его можно выполнить как чисто аналитически, так и численно, используя дискретное преобразование Фурье (далее FFT). Аналитическое решение сложнее и имеет очевидное ограничение на использование только тех функций, для которых известны Фурье-образы.
Что такое фильтр?
Фильтр – это схема, которая удаляет или «отфильтровывает» определенный диапазон частотных компонентов. Другими словами, он разделяет спектр сигнала на частотные составляющие, которые будут передаваться дальше, и частотные составляющие, которые будут блокироваться.
Если у вас нет большого опыта анализа частотной области, вы можете быть не уверены в том, что представляют собой эти частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.
Давайте представим, что у нас есть аудиосигнал, который состоит из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоида во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц. Теперь предположим, что мы включили генератор на 500 кГц, который вносит в аудиосигнал высокочастотный шум.
Сигнал, видимый на осциллографе, будет по-прежнему представлять собой только одну последовательность напряжений с одним значением на момент времени, но он будет выглядеть по-другому, поскольку его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокочастотные колебания шума.
Однако в частотной области синусоида и шум являются отдельными частотными компонентами, которые присутствуют одновременно в этом одном сигнале. Синусоидальная волна и шум занимают разные участки представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направив сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.
Рисунок 3 – Представление аудиосигнала и высокочастотного шума в частотной области
Типы фильтров
В зависимости от особенностей амплитудно-частотных характеристик фильтры можно распределить по широким категориям. Если фильтр пропускает низкие частоты и блокирует высокие частоты, он называется фильтром нижних частот. Если он блокирует низкие частоты и пропускает высокие частоты, это фильтр верхних частот. Существуют также полосовые фильтры, которые пропускают только относительно узкий диапазон частот, и режекторные фильтры, которые блокируют только относительно узкий диапазон частот.
Рисунок 4 – Амплитудно-частотные характеристики фильтров
Фильтры также могут быть классифицированы в соответствии с типами компонентов, которые используются для реализации схемы. Пассивные фильтры используют резисторы, конденсаторы и катушки индуктивности; эти компоненты не способны обеспечить усиление, и, следовательно, пассивный фильтр может только сохранять или уменьшать амплитуду входного сигнала. Активный фильтр, напротив, может фильтровать сигнал и применять усиление, поскольку он включает в себя активный компонент, такой как транзистор или операционный усилитель.
Рисунок 5 – Этот активный фильтр нижних частот основан на популярной топологии Саллена-Ки
В данной статье рассматривается анализ и проектирование пассивных фильтров нижних частот. Эти схемы играют важную роль в самых разных системах и приложениях.
RC фильтр нижних частот
Чтобы создать пассивный фильтр нижних частот, нам нужно объединить резистивный элемент с реактивным элементом. Другими словами, нам нужна схема, которая состоит из резистора и либо конденсатора, либо катушки индуктивности. Теоретически, топология фильтров нижних частот резистор-индуктивность (RL) эквивалентна, с точки зрения фильтрующей способности, топологии фильтров нижних частот резистор-конденсатор (RC). Однако на практике версия резистор-конденсатор встречается гораздо чаще, и, следовательно, оставшаяся часть этой статьи будет посвящена RC фильтру нижних частот.
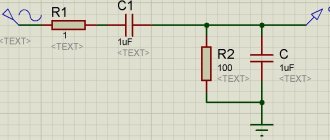
Рисунок 6 – RC фильтр нижних частот
Как вы можете видеть на схеме, пропускающая нижние частоты частотная характеристика RC фильтра создается путем установки резистора последовательно с путем прохождения сигнала и конденсатора параллельно нагрузке. На схеме нагрузка является отдельным компонентом, но в реальной цепи она может представлять что-то гораздо более сложное, например, аналого-цифровой преобразователь, усилитель или входной каскад осциллографа, который вы используете для измерения амплитудно-частотной характеристики фильтра.
Мы можем интуитивно проанализировать фильтрующее действие топологии RC фильтра нижних частот, если поймем, что резистор и конденсатор образуют частотно-зависимый делитель напряжения.
Рисунок 7 – RC фильтр нижних частот перерисован так, чтобы он выглядел как делитель напряжения
Когда частота входного сигнала низкая, полное сопротивление конденсатора будет высоким относительно полного сопротивления резистора; таким образом, большая часть входного напряжения падает на конденсаторе (и на нагрузке, которая параллельна конденсатору). Когда входная частота высокая, полное сопротивление конденсатора будет низким по сравнению с полным сопротивлением резистора, что означает, что на резисторе падает большее напряжение, и меньшее напряжение передается на нагрузку. Таким образом, низкие частоты пропускаются, а высокие частоты блокируются.
Это качественное объяснение работы RC фильтра нижних частот является важным первым шагом, но оно не очень полезно, когда нам нужно проектировать реальную схему, потому что термины «высокая частота» и «низкая частота» чрезвычайно расплывчаты. Инженеры должны создавать схемы, которые пропускают и блокируют определенные частоты. Например, в аудиосистеме, описанной выше, мы хотим сохранить сигнал 5 кГц и подавить сигнал 500 кГц. Это означает, что нам нужен фильтр, который переходит от пропускания к блокировке где-то между 5 кГц и 500 кГц.
Разбор фильтра с Алиэкспресс
Для того, чтобы вы уловили предыдущую мысль, мы разберем простой пример от наших узкоглазых братьев. На Алиэкпрессе продаются различные фильтры для сабвуфера. Рассмотрим один из них.
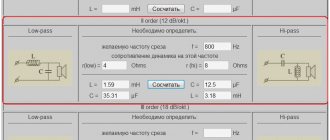
Как вы заметили, на нем написаны характеристики фильтра: данный тип фильтра рассчитан на сабвуфер мощностью 300 Ватт, наклон его характеристики 12 дБ/октаву. Если соединять к выходу фильтра саб с сопротивлением катушки в 4 Ома, то частота среза составит 150 Гц. Если же сопротивление катушки саба 8 Ом, то частота среза составит 300 Гц.
Для полных чайников продавец даже привел схему в описании товара. Выглядит она вот так:
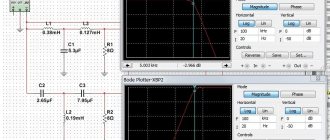
Далее мы собираем эту схему в Proteus. Так как при параллельном соединении конденсаторов номиналы суммируются, я сразу заменил 4 конденсатора одним.
Чаще всего можно увидеть прямо на динамиках значение сопротивления катушки на постоянном токе: 2 Ω, 4 Ω, 8 Ω. Реже 16 Ω. Значок Ω после цифр обозначает Омы. Также не забывайте, что катушка в динамике обладает индуктивностью.
Как ведет себя катушка индуктивности на разных частотах?
Как вы видите, на постоянном токе катушка динамика обладает активным сопротивлением, так как она намотана из медного провода. На низких частотах в дело вступает реактивное сопротивление катушки, которое вычисляется по формуле:
где
ХL — сопротивление катушки, Ом
П — постоянная и равна приблизительно 3,14
F — частота, Гц
L — индуктивность, Гн
Так как сабвуфер предназначен именно для низких частот, значит, оследовательно с активным сопротивлением самой катушки добавляется реактивное сопротивление этой же самой катушки. Но в нашем опыте мы это учитывать не будем, так как не знаем индуктивность нашего воображаемого динамика. Поэтому, все расчеты в опыте берем с приличной погрешностью.
Как утверждает китаец, при нагрузке на фильтр динамика в 4 Ома, его полоса пропускания будет доходить до 150 Герц. Проверяем так ли это:
Его АЧХ
Как вы видите, частота среза на уровне в -3 дБ составила почти 150 Герц.
Нагружаем наш фильтр динамиком в 8 Ом
Частота среза составила 213 Гц.
В описании на товар утверждалось, что частота среза на 8-омный саб составит 300 Гц. Думаю, можно поверить китайцам, так как во-первых, все данные приближенные, а во-вторых, симуляция в программах далека от реальности. Но суть опыта была не в этом. Как мы видим на АЧХ, нагружая фильтр сопротивлением большего номинала, частота среза сдвигается в большую сторону. Это также надо учитывать при проектировании фильтров.
Частота среза
Диапазон частот, для которого фильтр не вызывает значительного ослабления, называется полосой пропускания, а диапазон частот, для которых фильтр вызывает существенное ослабление, называется полосой задерживания. Аналоговые фильтры, такие как RC фильтр нижних частот, переходят из полосы пропускания в полосу задерживания всегда постепенно. Это означает, что невозможно идентифицировать одну частоту, на которой фильтр прекращает пропускать сигналы и начинает их блокировать. Однако инженерам нужен способ, чтобы удобно и кратко охарактеризовать амплитудно-частотную характеристику фильтра, и именно здесь в игру вступает понятие частоты среза.
Когда вы посмотрите на график амплитудно-частотной характеристики RC фильтра, вы заметите, что термин «частота среза» не очень точен. Изображение спектра сигнала, «разрезанного» на две половины, одна из которых сохраняется, а другая отбрасывается, неприменимо, поскольку затухание увеличивается постепенно по мере того, как частоты перемещаются от значений ниже частоты среза к значениям выше частоты среза.
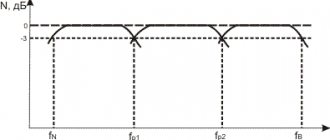
Частота среза RC фильтра нижних частот фактически является частотой, на которой амплитуда входного сигнала уменьшается на 3 дБ (это значение было выбрано, поскольку уменьшение амплитуды на 3 дБ соответствует снижению мощности на 50%). Таким образом, частоту среза также называют частотой -3 дБ, и на самом деле это название является более точным и более информативным. Термин полоса пропускания относится к ширине полосы пропускания фильтра, и в случае фильтра нижних частот полоса пропускания равна частоте -3 дБ (как показано на диаграмме ниже).
Рисунок 8 – Данная диаграмма показывает общие особенности амплитудно-частотной характеристики RC фильтра нижних частот. Ширина полосы пропускания равна частоте -3 дБ.
Как объяснялось выше, пропускающее низкие частоты поведение RC фильтра обусловлено взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора. Чтобы определить подробности амплитудно-частотной характеристики фильтра, нам нужно математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C); мы также можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (fср) RC фильтра нижних частот рассчитывается следующим образом:
\[f_{ср} = \frac{1}{2\pi RC}\]
Давайте посмотрим на простой пример. Значения конденсаторов являются более сдерживающими, чем значения резисторов, поэтому мы начнем с распространенного значения емкости (например, 10 нФ), а затем воспользуемся формулой для определения необходимого значения сопротивления. Цель состоит в том, чтобы разработать фильтр, который будет сохранять аудиосигнал 5 кГц и подавлять шум 500 кГц. Мы попробуем частоту среза 100 кГц, а позже в этой статье мы более тщательно проанализируем влияние этого фильтра на обе частотные составляющие.
\[100 \times 10^3 = \frac{1}{2 \pi R (10\times 10^{-9})} \\ \Rightarrow R=\frac{1}{2 \pi (10\times 10^{-9})(100 \times 10^3)} = 159,15 \ Ом\]
Таким образом, резистор 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который дает амплитудно-частотную характеристику, близкую к необходимой.
Расчет амплитудно-частотной характеристики фильтра
Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типового расчета делителя напряжения. Выходное напряжение резистивного делителя напряжения выражается следующим образом:
Рисунок 9 – Резистивный делитель напряжения
\[V_{вых} = V_{вх} \left( \frac{R_2}{R_1 + R_2} \right)\]
RC фильтр использует эквивалентную структуру, но вместо R2 у нас конденсатор. Сначала мы заменим R2 (в числителе) на реактивное сопротивление конденсатора (XC). Далее нам нужно рассчитать величину полного сопротивления и поместить его в знаменатель. Таким образом, мы имеем
\[V_{вых} = V_{вх} \left( \frac{X_C}{\sqrt{R_1^2+X_C^2}} \right)\]
Реактивное сопротивление конденсатора указывает величину противодействия протеканию тока, но, в отличие от активного сопротивления, величина противодействия зависит от частоты сигнала, проходящего через конденсатор. Таким образом, мы должны рассчитать реактивное сопротивление на определенной частоте, и формула, которую мы используем для этого, следующая:
\[X_C=\frac{1}{2 \pi f C}\]
В приведенном выше примере схемы R ≈ 160 Ом, и C = 10 нФ. Предположим, что амплитуда Vвх равна 1 В, поэтому мы можем просто удалить Vвх из расчетов. Сначала давайте рассчитаем амплитуду Vвых на частоте необходимой нам синусоиды:
\[X_{C\_5кГц} = \frac{1}{2 \pi (5000)(10 \times 10^{-9})}= 3183\ Ом\]
\[V_{вых\_5кГц} = \frac{3183}{\sqrt{3183^2+160^2}}= 0,999 \ В\]
Амплитуда необходимого нам синусоидального сигнала практически не изменяется. Это хорошо, поскольку мы намеревались сохранить синусоидальный сигнал при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше частоты синусоидального сигнала (5 кГц).
Теперь посмотрим, насколько успешно фильтр ослабит шумовую составляющую.
\[X_{C\_500кГц} = \frac{1}{2 \pi (500 \times 10^3)(10 \times 10^{-9})}= 31,8\ Ом\]
\[V_{вых\_500кГц} = \frac{31,8}{\sqrt{31,8^2+160^2}}= 0,195 \ В\]
Амплитуда шума составляет всего около 20% от первоначального значения.
Визуализация амплитудно-частотной характеристики фильтра
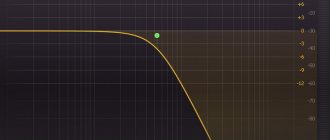
Наиболее удобным способом оценки влияния фильтра на сигнал является изучение графика его амплитудно-частотной характеристики. На этих графиках, часто называемых графиками Боде, амплитуда (в децибелах) откладывается по вертикальной оси, а частота – по горизонтальной оси; горизонтальная ось обычно имеет логарифмический масштаб, поэтому физическое расстояние между 1 Гц и 10 Гц такое же, как физическое расстояние между 10 Гц и 100 Гц, между 100 Гц и 1 кГц и так далее. Такая конфигурация позволяет нам быстро и точно оценить поведение фильтра в очень широком диапазоне частот.
Рисунок 10 – Пример графика амплитудно-частотной характеристики
Каждая точка на кривой указывает амплитуду, которую будет иметь выходной сигнал, если входной сигнал имеет величину 1 В и частоту, равную соответствующему значению на горизонтальной оси. Например, когда частота входного сигнала равна 1 МГц, амплитуда выходного сигнала (при условии, что амплитуда входного сигнала равна 1 В) будет 0,1 В (поскольку –20 дБ соответствует уменьшению в десять раз).
Общий вид этой кривой амплитудно-частотной характеристики станет вам очень знакомым, если вы будете проводить больше времени со схемами фильтров. Кривая почти идеально плоская в полосе пропускания, а затем, по мере приближения частоты входного сигнала к частоте среза, скорость ее спада начинает увеличиваться. В конечном итоге скорость изменения затухания, называемая спадом, стабилизируется на уровне 20 дБ/декада, то есть уровень выходного сигнала уменьшается на 20 дБ при каждом увеличении частоты входного сигнала в десять раз.
Оценка производительности фильтра нижних частот
Если мы построим амплитудно-частотную характеристику фильтра, который мы разработали ранее в этой статье, то увидим, что амплитудный отклик на 5 кГц, по сути, равен 0 дБ (т.е. почти нулевое затухание), а амплитудный отклик на 500 кГц составляет приблизительно –14 дБ (что соответствует коэффициенту передачи 0,2). Эти значения согласуются с результатами расчетов, которые мы выполнили в предыдущем разделе.
Поскольку RC фильтры всегда имеют плавный переход от полосы пропускания к полосе задерживания, а затухание никогда не достигает бесконечности, мы не можем разработать «идеальный» фильтр, то есть фильтр, который не влияет на необходимый синусоидальный сигнал и полностью устраняет шум. Вместо этого у нас всегда есть компромисс. Если мы сместим частоту среза ближе к 5 кГц, то получим большее затухание шума, но так же и большее затухание полезного синусоидального сигнала, который мы хотим отправить на динамик. Если мы переместим частоту среза ближе к 500 кГц, то получим меньшее затухание на частоте полезного сигнала, но так же и меньшее затухание на частоте шума.
Автотрансформаторное и трансформаторное включение
Желая получить более острую резонансную кривую, можно использовать трансформаторное (рис.3) или автотрансформаторное (рис.4) включение для подачи входного напряжения.
Рис. 3. Трансформаторное включение.
Рис. 4. Автотрансформаторное включение.
Число витков катушки связи (рис.З) или число витков отвода (считая от заземленного конца катушки) можно определить из формулы: R1 = Ro(N/No)^2 , где R1 — это фактически и есть выходное сопротивление источника входного переменного напряжения, Ro — сопротивление контура на резонансной частоте, N — число витков катушки связи (или число витков, от которых сделан отвод), No — число витков контурной катушки (или общее число витков катушки, если по рис.4).
Рис. 5. Емкостный автотрансформатор.
Совсем не обязательно делать отвод именно от катушки, можно сделать отвод и от конденсатора, вернее от емкостной составляющей контура. Так получится — емкостный автотрансформатор (рис. 5).
А соотношение емкостей для определенной величины выходного сопротивления источника сигнала можно определить из формулы: R1 = Ro * C1^2 / (C1+C2)^2.
На контур может оказывать шунтирующее влияние не только выходное сопротивление источника Uвх, но и входное сопротивление каскада, на который с контура поступает выходное напряжение Uвых (R2 на рис. 6). Особенно если входное сопротивление каскада (R2) невелико (сопоставимо или даже меньше Ro).
Рис. 6. Схема фильтра.
В этом случае необходимо сначала вычислить новое значение Ro, уменьшенное параллельным включением сопротивления R2. Расчет производить по известной формуле параллельных сопротивлений:
R = (RoR1) / (Ro+R2).
А потом уже рассчитывать согласование (взяв полученную величину R как Ro в формулах).
Фазовый сдвиг фильтра низких частот
До сих пор мы обсуждали способ, которым фильтр изменяет амплитуду различных частотных составляющих в сигнале. Однако реактивные элементы цепи в дополнение к влиянию на амплитуду всегда вносят сдвиг фазы.
Понятие фазы относится к значению периодического сигнала в определенный момент цикла. Таким образом, когда мы говорим, что схема вызывает сдвиг фазы, то имеем в виду, что она создает смещение между входным и выходным сигналами: входной и выходной сигналы больше не начинают и заканчивают свои циклы в один и тот же момент времени. Значение сдвига фазы, например, 45° или 90°, показывает, какое было создано смещение.
Каждый реактивный элемент в цепи вводит сдвиг фазы на 90°, но этот фазовый сдвиг происходит не сразу. Фаза выходного сигнала, так же как и амплитуда выходного сигнала, изменяется постепенно по мере увеличения частоты входного сигнала. В RC фильтре нижних частот у нас есть один реактивный элемент (конденсатор), и, следовательно, схема в конечном итоге будет вводить сдвиг фазы на 90°.
Как и в случае амплитудно-частотной характеристикой, фазо-частотную характеристику легче всего оценить, изучив график, на котором частота на горизонтальной оси приведена в логарифмическом масштабе. Приведенное ниже описание дает общее представление, а затем вы можете заполнить детали, изучив график.
- Сдвиг фазы изначально равен 0°.
- Он постепенно увеличивается до достижения 45° на частоте среза; на этом участке характеристики скорость изменения увеличивается.
- После частоты среза сдвиг фазы продолжает увеличиваться, но скорость изменения уменьшается.
- Скорость изменения становится очень малой, когда сдвиг фазы асимптотически приближается к 90 °.
Рисунок 11 – Сплошная линия – это амплитудно-частотная характеристика, а пунктирная линия – это фазо-частотная характеристика. Частота среза составляет 100 кГц. Обратите внимание, что на частоте среза сдвиг фазы составляет 45°.
Фильтры нижних частот второго порядка
До сих пор мы предполагали, что RC фильтр нижних частот состоит из одного резистора и одного конденсатора. Эта конфигурация является фильтром первого порядка.
«Порядок» пассивного фильтра определяется количеством реактивных элементов, то есть конденсаторов или индуктивностей, которые присутствуют в цепи. Фильтр более высокого порядка имеет больше реактивных элементов, что приводит к большему сдвигу фазы и более крутому спаду АЧХ. Эта вторая характеристика является основной причиной для увеличения порядка фильтра.
Добавляя один реактивный элемент к фильтру, например, переходя от первого порядка ко второму или от второго к третьему, мы увеличиваем максимальный спад на 20 дБ/декада. Более крутой спад приводит к более быстрому переходу от низкого затухания к высокому затуханию, и это может привести к улучшению производительности, когда нет широкой полосы частот, отделяющей необходимые частотные компоненты от шумовых компонентов.
Фильтры второго порядка обычно строятся вокруг резонансного контура, состоящего из катушки индуктивности и конденсатора (эта топология называется «RLC», т.е. резистор-индуктивность-конденсатор). Однако также возможно создание RC фильтров второго порядка. Как показано на рисунке ниже, всё, что нам нужно сделать, это включить каскадно два RC фильтра первого порядка.
Рисунок 12 – RC фильтр нижних частот второго порядка
Хотя эта топология, безусловно, создает характеристику второго порядка, она широко не используется – как мы увидим в следующем разделе, ее амплитудно-частотная характеристика часто уступает амплитудно-частотной характеристике активного фильтра второго порядка или RLC фильтра второго порядка.
Упрощенные формулы
Для простого расчета фильтров далее приведены упрощенные формулы, позаимствованные из инженерного справочника.
В формулах присутствует коэффициент 160000 (сто шестьдесят тысяч). Эта цифра возникает по двум причинам.
- Во-первых предполагается брать величину емкости при расчетах в микрофарадах (10-6 Фарада)
- Во-вторых при переходе от круговой частоты к цикличной возникает множитель 2π
Соответственно:
1 / (2⋅π⋅10-6) = 159154 ≈ 160000
Итак, давай те же перейдем к самим фильтрам.
Амплитудно-частотная характеристика RC фильтра второго порядка
Мы можем попытаться создать RC фильтр нижних частот второго порядка, разработав фильтр первого порядка в соответствии с необходимой частотой среза, а затем соединив два этих каскада первого порядка последовательно. Это даст фильтр, который имеет аналогичную общую амплитудно-частотную характеристику и максимальный спад 40 дБ/декада вместо 20 дБ/декада.
Однако если мы посмотрим на АЧХ более внимательно, то увидим, что частота –3 дБ снизилась. RC фильтр второго порядка ведет себя не так, как ожидалось, поскольку эти два звена не являются независимыми – мы не можем просто соединить эти две звена вместе и проанализировать схему как фильтр нижних частот первого порядка, за которым следует идентичный фильтр нижних частот первого порядка.
Кроме того, даже если мы вставим буфер между этими двумя звеньями, чтобы первое RC звено и второе RC звено могли работать как независимые фильтры, затухание на исходной частоте среза будет составлять 6 дБ вместо 3 дБ. Это происходит именно потому, что два звена работают независимо – первый фильтр вносит затухание 3 дБ на частоте среза, а второй фильтр добавляет еще 3 дБ затухания.
Рисунок 13 – Сравнение амплитудно-частотных характеристик фильтров нижних частот второго порядка
Основное ограничение RC фильтра нижних частот второго порядка состоит в том, что разработчик не может точно настроить переход от полосы пропускания к полосе задерживания, регулируя добротность (Q) фильтра; этот параметр указывает, насколько сглажена амплитудно-частотная характеристика. Если вы каскадно соединяете два идентичных RC фильтра нижних частот, общая передаточная функция соответствует отклику второго порядка, но добротность всегда равна 0,5. Когда Q = 0,5, фильтр находится на границе чрезмерного затухания, и это приводит к амплитудно-частотной характеристике, которая «провисает» в переходной области. Активные фильтры второго порядка и резонансные фильтры второго порядка не имеют такого ограничения; разработчик может управлять добротностью и, таким образом, точно настраивать амплитудно-частотную характеристику в переходной области.
Расчет пассивных разделительных фильтров в акустических системах
Данная статья поможет рассчитать электрические фильтры. Точность расчета высокая, но все же для точной подгонки АЧХ необходимо использовать микрофон, так как здесь АЧХ и импеданс условно считаются идеальными.
Разделительные фильтры с плоской АЧХ обладают рядом преимуществ перед фильтрами других типов, и являются наиболее употребляемыми в настоящее время в АС класса HI-FI. Поэтому в методике расчета будет рассмотрен только этот тип фильтров. Суть расчета состоит в том, что сначала разделительные фильтры рассчитываются из условия активной нагрузки и источника напряжения с бесконечно малым выходным сопротивлением (что справедливо для современных усилителей звуковой частоты). Затем принимаются меры, направленные на снижение влияния амплитудно-частотных и фазочастотных искажений громкоговорителей и комплексного характера их входного сопротивления на характеристики фильтров.
Расчет разделительных фильтров начинается с определения их порядка и нахождения параметров элементов лестничного фильтра прототипа нижних частот.
Фильтром-прототипом называется лестничный фильтр нижних частот, значения элементов которого нормированы относительно единичной частоты среза и единичной активной нагрузки. Рассчитав элементы фильтра нижних частот определенного порядка при реальной частоте и реальном значении сопротивления нагрузки, можно путем применения преобразования частоты определить схему и рассчитать значения элементов фильтра верхних частот и полосового фильтра соответствующего порядка. Нормированные значения элементов фильтра-прототипа, работающего от источника напряжения, определяются путем разложения в цепную дробь его выходной проводимости. Нормированные значения элементов фильтров-прототипов для расчета разделительных фильтров «всепропускающего типа с плоской АЧХ» 1…6-го порядка сведены в таблицу:
| Порядок фильтра | Значение нормированных параметров значения z | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 1,0 | – | – | – | – | – |
| 2 | 2,0 | 0,5 | – | – | – | – |
| 3 | 1,5 | 1,33 | 0,5 | – | – | – |
| 4 | 1,88 | 1,59 | 0,94 | 0,35 | – | – |
| 5 | 1,54 | 1,69 | 1,38 | 0,89 | 0,31 | – |
| 6 | 1,8 | 1,85 | 1,47 | 1,12 | 0,73 | 0,5 |
На рис.1 представлена схема фильтра-прототипа шестого порядка. Схемы фильтров прототипов меньших порядков образуются путем отбрасывания соответствующих элементов – α (начиная с больших) – например, фильтр-прототип 1-го порядка состоит из одной индуктивности α1 и нагрузки Rн.
Рис. 1. Схема односторонне нагруженного фильтра-прототипа нижних частот 6-го порядка
Значение реальных параметров элементов, соответствующих выбранному порядку разделительных фильтров, сопротивлению нагрузки Rн (Ом) и частоте среза (разделения) fd (Гц) рассчитываются следующим образом:
а) для фильтра нижних частот:
каждый элемент α-индуктивность фильтра-прототипа переводится в реальную индуктивность (Гн), рассчитываемую по формуле:
L=αRн/2πfd [1]
каждый элемент α-емкость фильтра-прототипа переводится в реальную емкость (Ф), рассчитываемую по формуле:
C=α/2πfdRн [2]
б) для фильтра верхних частот:
каждый элемент α-индуктивность фильтра-прототипа заменяется реальной емкостью рассчитываемой по формуле:
C=1/2πfdαRн [3]
каждый элемент α-емкость фильтра-прототипа заменяется реальной индуктивностью, рассчитываемой по формуле:
L=Rн/2πfdα [4]
в) для полосового фильтра:
каждый элемент α-индуктивность заменяется на последовательный контур, состоящий из реальных L и C-элементов, рассчитываемых по формулам
L=αRн/2π(fd2-fd1) [5]
где fd2 и fd1 – соответственно нижняя и верхняя частоты среза полосового фильтра,
С=1/4π2f02L [6]
где f0=√ fd1fd2 – средняя частота полосового фильтра.
Каждый элемент α-емкость заменяется на параллельный контур, состоящий из реальных L и C-элементов, рассчитываемых по формулам:
С=α/2π(fd2-fd1)Rн, [7]
L=1/4π2f02C [8]
Пример. Требуется рассчитать значения элементов раздельных фильтров для трехполосной АС.
Выбираем разделительные фильтры второго порядка. Пусть выбранные значения частот разделения составляют: между низкочастотным и среднечастотным каналом fd1=500 Гц, между среднечастотными и высокочастотными fd2=5000 Гц. Сопротивление громкоговорителей на постоянном токе: низкочастотного и среднечастотного – 8 Ом, высокочастотного – 16 Ом.
Рис. 2. Пример расчета разделительных фильтров трехполосной АС а) АЧХ громкоговорителей без фильтров; б) АЧХ громкоговорителей с фильтрами, цепями согласования и коррекции; в) суммарная АЧХ АС на рабочей оси и при смещении микрофона на угол ±10° в вертикальной плоскости
Амплитудно-частотные характеристики громкоговорителей, измеренные в заглушенной камере на рабочей оси АС на расстоянии 1 м, изображены на рис.2, а) (низкочастотный громкоговоритель 100ГД-1, среднечастотный 30ГД-8, высокочастотный 10ГД-43).
Рассчитаем фильтр нижних частот:
Значение нормированных параметров элементов определим из таблицы: α1=2,0, α2=0,5.
Из рис.1 определяем схему фильтра-прототипа нижних частот: фильтр состоит из индуктивности α1, емкости α2 и нагрузки Rн.
Значения реальных элементов фильтров нижних частот находим по выражениям [1] и [2]:
L1 НЧ=αRн/2πfd1=2,0·8,0/(2·3,14·500)=5,1 мГн,
C1 НЧ=α/2πfd1Rн=0,5/(2·3,14·500·8,0)=20 мкФ.
Значения элементов полосового фильтра (для среднечастотного громкоговорителя) определяем в соответствии с выражениями [5]…[8]:
L1 СЧ=α1Rн/2π(fd2-fd1)=2,0·8,0/2·3,14(5000-500)=0,566 мГн (сторона ВЧ)
С1 СЧ=1/4π2f02L1 СЧ=1/4·3,142·5000·500·5,66·10-4=18 мкФ (сторона НЧ)
С2 СЧ=α2/2π(fd2-fd1)Rн=0,5/2·3,14(5000-500)·8,0=2,2 мкФ (сторона ВЧ)
L2 СЧ=1/4π2f02C2 СЧ=1/4·3,142·5000·500·2,2·10-6=4,6 мГн (сторона НЧ)
Значения элементов фильтра верхних частот определяем в соответствии с выражениями [3] и [4]:
C1 ВЧ=1/2πfd2α1Rн=1/(2·3,14·5000·2,0·16)=1,00 мкФ,
L2 ВЧ=Rн/2πfd2α2=16/(2·3,14·5000·2,0)=0,25 мГн.
Для согласования фильтров с входным комплексным сопротивлением громкоговорителей может применяться специальная согласующая цепь. При отсутствии этой цепи входное сопротивление громкоговорителя оказывает влияние на АЧХ и ФЧХ разделительных фильтров. Параметры элементов согласующей цепи, включаемой параллельно громкоговорителю, находятся из условия:
Yc(s)+YГР(s)=1/RE,
где Yc(s) – проводимость согласующей цепи, YГР(s) – входная проводимость громкоговорителя, RE – электрическое сопротивление громкоговорителя на постоянном токе.
Схема согласующей цепи изображена на рис.3. Цепь является дуальной по отношению к эквивалентной электрической схеме громкоговорителя. Значения элементов цепи определяем следующим образом:
RK1=RE, [9]
CK1=LVC/RE2 [10]
RK= RE2/RES=QESRE/QMS,
CK=LCES/ RE2=1/QESRE2πfs,
LK=CMES RE2=QESRE/2πfs,
где LVC – индуктивность звуковой катушки, fs, CMES, LCES, RES – электромеханические параметры громкоговорителя.
Для компенсации входного сопротивления низкочастотного громкоговорителя применяют упрощенную цепь, состоящую из последовательно включенных сопротивления RK1 и емкости CK1. Это объясняется тем, что механический резонанс громкоговорителя не оказывает влияния на характеристики фильтра нижних частот и компенсируется только индуктивный характер входного сопротивления громкоговорителя. Целесообразность подключения полной согласующей цепи к высокочастотным и среднечастотным громкоговорителям оправдана в том случае, если резонансная частота громкоговорителя находится вблизи частоты среза фильтра верхних частот или нижней частоты среза полосового фильтра. В том случае, если частоты среза фильтров значительно выше резонансных частот громкоговорителей, включение упрощенной цепи является достаточным.
Рис.3. Схема согласующей цепи для компенсации комплексного характера входного сопротивления громкоговорителя
Влияние входного комплексного сопротивления громкоговорителей можно рассмотреть на примере разделительных фильтров второго порядка верхних и нижних частот [3] (рис.4).
Рис. 4. Электрическая эквивалентная схема громкоговорителя с разделительными фильтрами 2-го порядка: а – с фильтром нижних частот; б – с фильтром верхних частот; (1 – фильтр; 2 – громкоговоритель)
Параметры НЧ громкоговорителя выбраны таким образом, что его АЧХ соответствует аппроксимации по Баттерворту, т.е. полная добротность Qts=0,707. Частота среза фильтра нижних частот выбрана в 10 раз больше резонансной частоты громкоговорителя fd=10fs. Индуктивность звуковой катушки выбрана из условия: QVC=0,1, где QVC – добротность звуковой катушки, определяемая как:
QVC=LVC2πfs/RE,
где fs – резонансная частота громкоговорителя, RE – сопротивление звуковой катушки на постоянном токе, LVC – индуктивность звуковой катушки.
Значение QVC=0,1 соответствует среднестатистическому значению индуктивности звуковой катушки мощных низкочастотных громкоговорителей. Вследствие этого можно считать, что индуктивность звуковой катушки LVC и активное сопротивление RE включены параллельно емкости фильтра C1 и образуют в области частоты среза фильтра широкий максимум АЧХ входного сопротивления, за которым следует острый провал (рис.5,а). Соответствующие изменения АЧХ фильтра по напряжению заключаются в небольшом подъеме АЧХ на частоте f≈2fs (вследствие индуктивности звуковой катушки) и плавном провале, за которым следует резкий пик АЧХ из-за резонанса цепи, образуемой индуктивностью звуковой катушки и емкостью разделительного фильтра. Соответствующие изменения АЧХ и ZBX после включения согласующей цепи из последовательно включенного резистора и конденсатора показаны на рис.5,а (кривые 2, 4, 6). Включение согласующей цепи приближает характер входного сопротивления громкоговорителя к активному и АЧХ разделительного фильтра по напряжению к желаемому. Однако вследствие влияния индуктивности звуковой катушки АЧХ по звуковому давлению отличается от желаемой (кривая 4), поэтому даже после согласующей цепи иногда требуется небольшая подстройка элементов фильтров и цепи согласования.
Рис. 5 АЧХ и входное сопротивление разделительных фильтров 2-го порядка, нагруженных на громкоговоритель: а) фильтр нижних частот; б) фильтр верхних частот;
- АЧХ по напряжению на выходе фильтра без согласующей цепи;
- АЧХ по напряжению на выходе фильтра с согласующей цепью;
- АЧХ по звуковому давлению без согласующей цепи;
- АЧХ по звуковому давлению с согласующей цепью;
- входное сопротивление фильтра с громкоговорителем без согласующей цепи;
- входное сопротивление фильтра с громкоговорителем с согласующей цепью.
В случае фильтра верхних частот влияние комплексного характера входного сопротивления громкоговорителя на входное сопротивление и АЧХ фильтра носит иной характер. Если частота среза фильтра верхних частот находится вблизи частоты резонанса громкоговорителя fs (случай, иногда встречающийся в фильтрах для среднечастотных громкоговорителей, но практически невозможный для высокочастотных громкоговорителей), входное сопротивление фильтра верхних частот с громкоговорителем без согласующей цепи может иметь глубокий провал вследствие того, что на частоте резонанса громкоговорителя fs его входное сопротивление значительно возрастает и имеет чисто активный характер. Фильтр оказывается как бы на холостом ходу, из-за резкого возрастания сопротивления нагрузки и его входное сопротивление определяется последовательно включенными элементами C1, L1. Чаще встречается ситуация, когда частота среза фильтра верхних частот fd значительно выше частоты резонанса громкоговорителя fs. На рис.5,б дан пример влияния входного сопротивления громкоговорителя и его компенсации на АЧХ фильтра верхних частот по напряжению и звуковому давлению. Частота среза фильтра выбрана значительно выше частоты резонанса громкоговорителя fd≈8 fs, параметры громкоговорителя QTS=1,5, QMS=10, QVC=0,08. Подъем АЧХ по звуковому давлению и напряжению в высокочастотной области, сопровождаемый провалом входного сопротивления, объясняется влиянием индуктивности звуковой катушки LVC. На более высоких частотах АЧХ падает, а входное сопротивление растет за счет возрастания индуктивного сопротивления звуковой катушки.
Кривые 2, 4, 6 на рис.5,б показывают влияние согласующей RC-цепи.
Выходное сопротивление разделительного фильтра верхних частот, растущее с понижением частоты, оказывает влияние на электрическую добротность громкоговорителя, увеличивая ее, и соответственно увеличивает полную добротность и форму АЧХ по звуковому давлению. Иными словами, имеет место эффект «раздемпфирования» громкоговорителя. Для набежания этого необходимо выбирать крутизну спада АЧХ фильтра и частоту среза фильтра верхних частот fd>>fs так, чтобы на частоте резонанса fs ослабление сигнала было не менее 20 дБ.
При расчете разделительных фильтров в примере, рассмотренном выше, принималось, что характер нагрузки – активный, поэтому рассчитаем согласующие цепи, компенсирующие комплексный характер входного сопротивления громкоговорителя.
Частота разделения низкочастотного и среднечастотного каналов fd1 выбрана примерно на две октавы выше резонансной частоты среднечастотного громкоговорителя, а частота разделения среднечастотного и высокочастотного каналов fd2 – на две октавы выше резонансной частоты высокочастотного громкоговорителя. Кроме того, можно принять, что индуктивность звуковой катушки высокочастотного громкоговорителя пренебрежимо мала в рабочем диапазоне частот и ей можно пренебречь (это справедливо для большинства высокочастотных громкоговорителей). В этом случае можно ограничиться применением упрощенной согласующей цепи для низкочастотного и среднечастотного громкоговорителей.
Пример. Измеренные (или определенные из кривой АЧХ входного сопротивления) индуктивности звуковых катушек: низкочастотного громкоговорителя LVC=3·10-3Г=3 мГн, среднечастотного громкоговорителя LVC=0,5·10-3 Г=0,5 мГн. Тогда значение элементов компенсирующих цепей рассчитывают по формулам [9] и [10]:
для НЧ: RK1–Rπ=8 Ом; СК1=LVC/R2E=3·10-3/64=47 мкФ
для СЧ: R’K1=RE-8 Ом; С’К1=LVC/R2E=0,5·10-3/64=8,0 мкФ.
На АЧХ среднечастотного громкоговорителя имеется пик, увеличивающий неравномерность суммарной АЧХ АС (рис.2,а); в этом случае целесообразно включить амплитудный корректор. Режектирующее звено (рис.6) применяется для коррекции пиков АЧХ громкоговорителей или всей АС. Это звено имеет чисто активное входное сопротивление, равное сопротивлению нагрузки RH и поэтому может быть включено между фильтром и громкоговорителем с скомпенсированным входным сопротивлением. В случае включения режектирующего звена на входе АС схема может быть упрощена, так как отпадает необходимость в элементах Cq, Lq, Rq, обеспечивающих активный характер входного сопротивления звена. Значения элементов рассчитываются по формулам:
RK≈RH(10-0,05N-1),
LK=RK∆f/2πf02,
CK=1/LK4π2f02,
Cq=LK/RH2,
Lq=CKRH2,
Rq=RH(1+ RH/RK),
где RH – сопротивление громкоговорителя (скомпенсированное) или входное сопротивление АС (Ом) в области резонансной частоты режектирующего звена;
∆f – полоса частот корректируемого пика АЧХ (отсчитывается по уровню – 3 дБ), Гц;
f0 – резонансная частота режектора, Гц;
N – величина пика АЧХ, дБ.
Рис. 6. Режектирующее звено: а) принципиальная схема; б) АЧХ
Применим режектирующее звено, включенное между фильтром и среднечастотным громкоговорителем с согласующей цепью.
Из АЧХ среднечастотного громкоговорителя определяем ∆f=1850 Гц, f0=4000 Гц, N=6 дБ. Сопротивление среднечастотного громкоговорителя с согласующей цепью RH=8 Ом.
Значения элементов режектирующего звена следующее:
RK≈RH(10-0,05N-1)=8(10-0,05·6-1)=7,96 Ом,
LK=RK∆f/2πf02=7,96·1850/2π(4000)2=0,147 мГн,
CK=1/LK4π2f02=1/1,47·10-4(2π4000)2=11мкФ,
Cq=LK/RH2=1,47·10-4/64=2,3 мкФ,
Lq=CKRH2=10,8·10-6·64=0,7 мГн,
Rq=RH(1+ RH/RK)=8(1+8/7,96)≈16,0 Ом.
В рассматриваемом примере АЧХ высокочастотного и среднечастотного громкоговорителя имеют средние уровни примерно на 6 дБ и соответственно 3 дБ выше, чем АЧХ низкочастотного громкоговорителя (запись звукового давления осуществлялась при подаче на все громкоговорители синусоидального напряжения одинаковой величины). В этом случае для уменьшения неравномерности суммарной АЧХ АС необходимо ослабить уровень среднечастотных и высокочастотных составляющих. Это можно сделать либо с помощью корректирующего высокочастотного звена первого порядка (рис.7), элементы которого рассчитываются по формулам:
RK≈RH(10-0,05N-1),
LK=RK/2πfd√(100,1N-2), N≥3 дБ,
Либо с помощью Г-образных пассивных аттенюаторов, обеспечивающих заданный уровень ослабления N (дБ) и заданное входное сопротивление RBX (рис.8). Значение элементов аттенюатора рассчитываем по формулам:
R1≈RBX(1-10-0,05N),
R2≈RHRBX10-0,05N/(RH–RBX10-0,05N).
Рис. 7. Звено 1-го порядка, корректирующее высокие частоты: а) принципиальная схема; б) АЧХ
Рис. 8. Пассивный Г-образный аттенюатор
Рассчитаем для примера значения элементов аттенюатора для ослабления на 6 дБ сигнала высокочастотного громкоговорителя. Пусть входное сопротивление громкоговорителя с включенным аттенюатором равняется входному сопротивлению громкоговорителя, т.е. 16 Ом, тогда:
R1≈16(1-10-0,05·6)≈8,0 Ом, R2≈16·10-0,05·6/(1-10-0,05·6)≈16,0 Ом.
Аналогично рассчитаем значения элементов аттенюатора для среднечастотного громкоговорителя: R1=4,7 Ом, R2=39 Ом. Аттенюаторы включаются сразу после громкоговорителей с согласующими цепями.
Полная схема разделительных фильтров изображена на рис.9, АЧХ АС с рассчитанными фильтрами – на рис.2,в.
Как было сказано выше, фильтры четных порядков допускают только один вариант полярности включения громкоговорителей, в частности, фильтры второго порядка требуют включения в противофазе. Для рассматриваемого примера низкочастотный и высокочастотный громкоговоритель должны иметь идентичную полярность включения, а среднечастотный – обратную. Требования к полярности включения громкоговорителей рассматривались выше на модели АС с идеальными громкоговорителями. Поэтому при включении реальных громкоговорителей, имеющих собственную ФЧХ≠0, (в случае выбора частот разделения вблизи граничных частот рабочего диапазона громкоговорителей или при большой неравномерности АЧХ громкоговорителей) условие согласования реальных ФЧХ каналов может не соблюдаться. Поэтому для контроля реальной ФЧХ по звуковому давлению громкоговорителей с фильтрами необходимо пользоваться фазометром с линией задержки или определять условие согласования косвенно по характеру суммарной АЧХ АС в полосах разделения каналов. Правильной полярностью включения громкоговорителей можно считать ту, которая соответствует меньшей неравномерности суммарной АЧХ в полосе разделения каналов. Точное согласование ФЧХ разделяемых каналов при удовлетворении всем остальным требованиям (плоская АЧХ и т.д.) осуществляется численными методами синтеза оптимальных разделительных фильтров-корректоров на компьютере.
Рис.9. Принципиальная электрическая схема АС с рассчитанными разделительными фильтрами (емкости в микрофарадах, индуктивности – в миллигенри, сопротивления – в омах).
В разработке пассивных разделительных фильтров важную роль играет их конструкция, а также выбор типа конкретных элементов – конденсаторов, катушек индуктивности, резисторов, в частности, большое влияние на характеристики АС с фильтрами оказывает взаимное размещение катушек индуктивности, при их неудачном расположении вследствие взаимной связи возможны наводки сигнала между близко расположенными катушками. По этой причине их рекомендуется располагать взаимно перпендикулярно, только такое расположение позволяет свести к минимуму их влияние друг на друга. Катушки индуктивности являются одним из важнейших компонентов пассивных разделительных фильтров. В настоящее время многие зарубежные фирмы применяют катушки индуктивности на сердечниках из магнитных материалов, обеспечивающих большой динамический диапазон, низкий уровень нелинейных искажений и малые габариты катушек. Однако конструирование катушек с магнитными сердечниками связано с применением специальных материалов, поэтому до настоящего времени многие разработчики применяют катушки с воздушными сердечниками, основные недостатки которых – большие габариты при условии малых потерь (особенно в фильтре низкочастотного канала), а также большой расход меди; достоинства – пренебрежимо малые нелинейные искажения.
Конфигурация катушки индуктивности с воздушным сердечником, изображенная на рис.10, является оптимальной, так как она обеспечивает максимальное отношение L/R, т.е. катушка с заданной индуктивностью L, намотанная проводом выбранного диаметра, имеет при данной конфигурации намотки наименьшее сопротивление R или наибольшую добротность по сравнению с любой другой. Отношение L/R, имеющее размерность времени, связано с размерами катушки соотношением [3.13]:
L/R=161,7alc/(6a+9l+10c);
L – в микрогенри, R – в омах, a, l, c – в миллиметрах.
Рис.10. Катушка индуктивности с воздушным сердечником оптимальной конфигурации: а) в разрезе; б) внешний вид.
Расчетные соотношения для данной конфигурации катушки: a=1,5с, l=c; конструктивный параметр катушки c=√(L/R8,66), число витков N=19,88√(L/c), диаметр провода в миллиметрах, d=0,841c/√N, масса провода (материал – медь) в граммах, q=c3/21, длина провода в миллиметрах, B=187,3√Lc. В том случае, если катушка индуктивности рассчитывается, исходя из провода данного диаметра, основные расчетные соотношения выглядят следующим образом:
конструктивный параметр c=5√(d419,882L/0,8414)=3,85√(d4L), сопротивление провода R=L/c28,66.
Найдем, для примера параметры катушки индуктивности рассчитанного ранее фильтра нижних частот. Индуктивность катушки составляет L1НЧ=5,1 мГ. Сопротивление R катушки на постоянном токе определим из допустимого затухания сигнала, вносимого реальной катушкой на низких частотах. Пусть ослабление сигнала за счет потерь R в катушке составляет N≤1дБ. Поскольку сопротивление низкочастотного громкоговорителя на постоянном токе составляет RE=8 Ом, то допустимое сопротивление катушки, определяемое из выражения R≤RE(100,05N-1), составляет R≤0,980 Ом; тогда конструктивный параметр катушки c=√5100/0,98·8,66=24,5 мм; количество витков N=19,8√(5100/24,5)=287 витков; диаметр провода d=0,841·24,5/√287=1,2 мм; масса провода q=24,53/21,4≈697 г; длина провода B=187,3√(85,1·24,5)≈46 м.
Другим важным элементом пассивных разделительных фильтров являются конденсаторы. Обычно в фильтрах используют бумажные или пленочные конденсаторы. Из бумажных наиболее употребляемые отечественные конденсаторы МБГО. Достоинством этих типов конденсаторов являются малые потери, высокая температурная стабильность, недостатком – большие габариты, снижение допустимого максимального напряжения на высоких частотах. В настоящее время в фильтрах ряда зарубежных АС используют электролитические неполярные конденсаторы с малыми внутренними потерями, объединяющие достоинства рассмотренных конденсаторов и свободные от их недостатков.
По материалам из книги: «Высококачественные акустические системы и излучатели»
(Алдошина И.А., Войшвилло А.Г.)
Резюме
- Все электрические сигналы содержат смесь необходимых частотных компонентов и нежелательных частотных компонентов. Нежелательные частотные компоненты обычно вызваны шумом и помехами, и в некоторых ситуациях они отрицательно влияют на производительность системы.
- Фильтр – это схема, которая по-разному реагирует на разные части спектра сигнала. Фильтр нижних частот предназначен для пропускания низкочастотных компонентов и блокирования высокочастотных компонентов.
- Частота среза фильтра нижних частот указывает частотную область, в которой фильтр переходит от низкого затухания к существенному затуханию.
- Выходное напряжение RC фильтра нижних частот можно рассчитать, рассматривая схему как делитель напряжения, состоящий из (независимого от частоты) активного сопротивления и (зависимого от частоты) реактивного сопротивления.
- График амплитуды выходного сигнала (в дБ на вертикальной оси) в зависимости от частоты (в герцах в логарифмическом масштабе на горизонтальной оси) является удобным и эффективным способом проверки теоретического поведения фильтра (амплитудно-частотная характеристика). Вы также можете использовать график зависимости фазы выходного сигнала от частоты в логарифмическом масштабе, чтобы определить величину сдвига фазы, которая будет применяться к входному сигналу (фазо-частотная характеристика).
- Фильтр второго порядка обеспечивает более крутой спад; эта характеристика второго порядка полезна, когда сигнал не обеспечивает широкую полосу разделения между необходимыми частотными компонентами и нежелательными частотными компонентами.
- Вы можете создать RC фильтр нижних частот второго порядка, создав два идентичных RC фильтра нижних частот первого порядка, а затем подключив выход одного к входу другого. Итоговая частота –3 дБ будет ниже ожидаемой.
Оригинал статьи:
- Robert Keim. What Is a Low Pass Filter? A Tutorial on the Basics of Passive RC Filters
▍ Аналитическое решение
Озвученным выше требованиям гладкости и симметрии (но не фазолинейности) соответствует фильтр Линквитца-Рейли. Зная формулу АЧХ , где — порядок фильтра, формулу импульсной характеристики можно получить аналитически через интеграл Фурье, а конкретные отсчёты FIR фильтра считать непосредственным её вычислением.
График фильтра в логарифмическом масштабе:
Лучший способ для вычисления интеграла Фурье — это использовать какую-нибудь систему компьютерной алгебры. Например, в Wolfram Mathematica это будет выглядеть так:
InverseFourierTransform[1/(1 + w^2), w, x] // FullSimplify ↓
График получившейся функции, она же импульсная характеристика:
Как видно из формулы и графика, импульсная характеристика бесконечна — стремится к нулю, но не достигает его; а также симметрична относительно нуля (за счёт фазолинейности). Ограничение её во времени осуществляется путём умножения на оконную функцию, за счёт чего значения функции за пределами окна приобретают нулевые значения, не требующих участия в расчётах. Побочным эффектом этого становится искажения исходного спектра фильтра — поскольку при умножении функций их спектры сворачиваются. Итоговый спектр можно увидеть также через преобразование Фурье. Например, для прямоугольного окна получим
в результате чего АЧХ фильтра изменится на
код
FourierTransform[E^-Abs[x] Sqrt[Pi/2] UnitBox[x/5], x, w] // FullSimplify ↓
Пульсации, которые мы видим, являются следствием от наличия «боковых лепестков» оконной функции. Их можно уменьшить, взяв более гладкое и широкое окно. Среди множества разработанных окон одним из наиболее оптимальных и удобным для аналитических вычислений является окно Нуттала, определяемое как
Примечание
Используя полиномы Чебышёва, окно Нуттала также можно вычислить как , где
Помножив её на импульсную характеристику фильтра, получим:
а АЧХ примет вид
код
frnw = FourierTransform[E^-Abs[x] Sqrt[Pi/2] NuttallWindow[x/20], x, w] // Simplify ↓
Как видно, величина пульсаций значительно уменьшилась. По графику видно, что «полка» фильтра слегка опустилась — в идеале это тоже нужно учитывать и компенсировать. В данном случае она составила (на нулевой частоте):
FourierTransform[E^-Abs[x] Sqrt[Pi/2] NuttallWindow[x/20], x, w] /.w->0.0 ↓
Мнимая часть здесь получилась вследствие погрешности при численных вычислениях и её можно смело отбрасывать (об этом говорит значение , поскольку точность вычислений в формате double и представляет примерно 16 десятичных цифр).
Аналогичным образом можно посчитать импульсные характеристики и для более высоких (но только целых) порядков, например:
InverseFourierTransform[1/(1+w^4), w, x] // FullSimplify ↓
Как видно, автоматического упрощения уже недостаточно и здесь требуется ручная работа по приведению формулы к удобочитаемому виду. В итоге получается следующая формула (в комплексных числах) для импульсной характеристики фильтра Линквитца-Рейли произвольного порядка:
При вычислении за счёт сложения комплексно-сопряжённых чисел мнимая часть обнуляется и в результате получится чисто действительная функция. Эту формулу можно выписать и непосредственно в действительных числах: