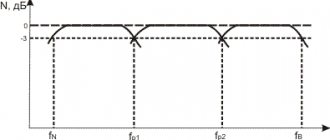
RC-цепь, такое частое явление радиоэлектроники. Такие фильтры стоят повсюду. Понимание того, как какой фильтр влияет на форму АЧХ сигнала во многом определяет правильность чтения всей электронной схемы. В статье собраны 5 основных RC-фильтров, приведены их АЧХ и упрощенные формулы расчета.
В ранние годы развития радиоэлектроники для воздействие на Амплитудно — Частотную Характеристику (АЧХ) сигнала в основном применялись LC — фильтры, т.е. фильтры состоящие из катушки индуктивности и конденсатора. Со временем им на смену пришла RC-цепь, которая была плотно взята в оборот радиоэлектроникой ввиду меньшей стоимости и габаритов.
Конечно, фильтры на RC-цепях не могут полностью вытеснить LC собратьев. Например в фильтрах для АС предпочтительнее использование LC-фильтров. Но практически во всей маломощной электронике главенствуют именно RC-цепи. Например двойная RC-цепь в фильтре RIAA-корректора.
Интересным вариантом избавления от катушек являются фильтры на гираторах, где посредством конденсатора и операционного усилителя эмитируется работа катушки.
Упрощенные формулы
Для простого расчета фильтров далее приведены упрощенные формулы, позаимствованные из инженерного справочника.
В формулах присутствует коэффициент 160000 (сто шестьдесят тысяч). Эта цифра возникает по двум причинам.
- Во-первых предполагается брать величину емкости при расчетах в микрофарадах (10-6 Фарада)
- Во-вторых при переходе от круговой частоты к цикличной возникает множитель 2π
Соответственно:
1 / (2⋅π⋅10-6) = 159154 ≈ 160000
Итак, давай те же перейдем к самим фильтрам.
ПЕРЕДАТОЧНАЯ ФУНКЦИЯ
Под передаточной функцией фильтра понимается отношение комплексной амплитуды напряжения на выходе фильтра к комплексной амплитуде напряжения на входе. Обычно передаточные функции физически реализуемых и устойчивых линейных цепей описываются в виде математических формул, знаменатели которых являются выражениями следующего вида (полиномами): Gn(s) = ansn+a n-1sn-1+…….+a1s+1. Порядок фильтра определяется степенью n от комплексной частоты s, которая связана с обычной круговой частотой как s = jω. (величина j называется мнимой единицей ). Выбор вида коэффициентов аn определяет принадлежность фильтров к типу Баттерворта, Чебышева и др. Например, полиномы Баттерворта разных порядков имеют вид В1 (s) = (1+s); B2 (s) = (1+1,414s+s2) и т. д.
В акустических системах проблема выбора фильтров усложняется тем, что необходимо выбрать три или два (в зависимости от количества полос) типа фильтров одинаковых или разных порядков, которые совместно с громкоговорителями обеспечивали бы суммарные характеристики акустической системы (такие как амплитудно-частотная характеристика — АЧХ, фазочастотная характеристика — ФЧХ, групповое время задерживания — ГВЗ, и др.) с требуемыми параметрами внутри эффективно-воспроизводимого диапазона частот.
История создания фильтров История создания разделительных фильтров начинается одновременно с появлением многополосных акустических систем. Одну из первых теорий разработали в 30-е годы инженеры G. A. Campbell и О. J. Zobel из фирмы Bell Labs (США). Первые публикации относятся к этому же периоду, их авторы K. Hilliard и H. Kimball работали в звуковом отделе фирмы Metro Goldwin Meyer. В 1936 году в мартовском номере Academy Research Council Technical Bulletin была опубликована их статья «Разделительные фильтры для громкоговорителей». В январе 1941 года K. Hilliard в журнале Electronics Magazine также опубликовал работу «Разделительные фильтры громкоговорителей», содержавшую все необходимые формулы для создания цепей Баттерворта первого и третьего порядков (как для параллельных, так и для последовательных схем). К 50-м годам фильтры Баттерворта были признаны предпочтительными для разделительных целей акустических систем. Тогда же в 60-х J. R. Ashley и R. Small впервые описали свойства «всепропускающих» фильтрующих схем, а также линейно-фазовых цепей.
Выяснению количественного соотношения затухания, вносимого фильтрами вне полосы пропускания, и величины интермодуляционных искажений вследствие перекрывания полос акустических систем, была посвящена статья «Фильтрующие цепи и модуляционные искажения» (автор R. Small), опубликованная в JAES в 1971 году. В ней было показано, что минимальная величина затухания должна быть 12 дБ/окт, чтобы предотвратить искажения в полосе перекрытия. Тогда же Ashley и L. М. Неnnе исследовали «всепропускающие» и «фазокогерентные» свойства фильтров Баттерворта третьего порядка. В 1976 году S. Linkwitz исследовал полярную диаграмму направленности для двухполосных систем с разнесенными излучателями и убедился, что акустические системы с разделительными фильтрами Линквитца-Риле обеспечивают ее симметричность.
Чуть позднее P. Garde дал полное описание всепропускающих фильтров и их разновидностей. Используя его идеи, D. Fink в соавторстве с Е. Long развил метод коррекции горизонтального (то есть глубинного) смещения головок громкоговорителей в акустических системах путем введения линий задержки в фильтр. Существенный вклад в теорию фильтрации внесли W. Marshall-Leach и R. Bullock, которые впервые ввели понятие оптимизации фильтров по типу и порядку с учетом смещения головок по двум осям. В продолжение этих работ R. Bullock описал свойства трехполосных симметричных фильтров и доказал, что трехполосная система фильтров не может быть получена как простая комбинация двухполосных, вопреки бытовавшему мнению. S. Lipshitz и J. Vanderkooy в серии статей рассмотрели различные варианты построения фильтров с минимально фазовыми характеристиками.
Новый этап в исследовании и проектировании многополосных акустических систем с разделительными фильтрами наступил с началом активной компьютеризации расчетов на основе программ ХОРТ, CACD, CALSOB, Filter Designer, LEAP 4.0 и др.
До недавнего времени конструирование разделительных фильтров в акустических системах шло практически методом «проб и ошибок». Это объясняется тем, что все теоретические работы прошлых лет, посвященные расчету разделительных фильтров в акустических системах, исходили из условия идеальности самих громкоговорителей. При анализе свойств разделительных фильтров того или иного типа и рассмотрении их влияния на характеристики акустических систем пренебрегали направленными свойствами громкоговорителей и условиями их физического размещения в корпусе акустической системы. Считали, что громкоговорители обладают плоской АЧХ, не вносят фазовых сдвигов в воспроизводимый сигнал и имеют активное входное сопротивление. Вследствие сказанного разработчики часто сталкивались с тем, что разделительные фильтры, обеспечивающие в идеализированных условиях требуемые характеристики, оказывались неприемлемыми при работе с реальными громкоговорителями, имеющими собственные амплитудно-частотные и фазочастотные искажения, комплексное входное сопротивление и обладающими направленными свойствами. Это и явилось причиной интенсификации в последние годы работ по созданию оптимизационных методов расчета разделительных фильтров-корректоров.
Выбор частот разделения Как уже было отмечено, разделительные фильтры оказывают существенное влияние на такие характеристики многополосных акустических систем, как АЧХ, ФЧХ, ГВЗ, характеристики направленности, распределение мощности входного сигнала между излучателями, входное сопротивление акустической системы, уровень нелинейных искажений.
Начальным этапом в проектировании разделительных фильтров в многополосных акустических системах является обоснованный выбор частот разделения (частот среза) низкочастотного, средне-частотного и высокочастотного каналов. При выборе частот разделения обычно используют следующие предпосылки.
1. Обеспечение возможно более равномерных характеристик направленности, то есть отсутствия «скачков» ширины диаграммы направленности при переходе от низкочастотного к среднечастотному и от средне- к высокочастотному громкоговорителю, поскольку в той области частот, где они работают вместе, при отсутствии фильтра, диаграмма направленности резко сужается за счет расширения площади излучения.
2. Сохранение плавного изменения ширины характеристики направленности (по той же причине). Громкоговорители стараются размещать как можно ближе друг к другу и располагать их друг над другом в вертикальной плоскости (что позволяет избежать искажений характеристики направленности в горизонтальной плоскости, так как это отрицательно сказывается на воспроизведении стереопанорамы). Если выбор частоты разделения и расстояния между громкоговорителями влияет на ширину характеристики направленности, то соотношение фаз и амплитуд сигналов разделяемых частотных каналов влияет на ориентацию характеристики направленности в пространстве. Различные типы фильтров, как будет показано далее, в разной степени влияют на наклон характеристики направленности в пространстве в области частот разделения.
3. Ослабление пиков и провалов на АЧХ громкоговорителей, возникающих из-за потери поршневого характера движения диффузора. Выбор частоты среза и крутизны спада АЧХ фильтров для низкочастотных и среднечастотных громкоговорителей стараются осуществлять таким образом, чтобы первые резонансные пики и провалы ослаблялись не менее, чем на 20 дБ.
4. Ограничение амплитуды смещения подвижных систем средне- и высокочастотных громкоговорителей в низкочастотной части излучаемого ими спектра (и, соответственно, подводимой мощности) до значений, определяемых их механической и тепловой прочностью, что повышает надежность их работы и снижает уровень нелинейных искажений. Эти задачи регулируются как выбором частоты среза, так и выбором крутизны среза, которая должна составлять не менее 12 дБ/окт.
5. Обеспечение требуемого уровня звукового давления, поскольку с повышением частоты среза в области высоких частот можно увеличить уровень подаваемого напряжения, например, на высокочастотный громкоговоритель (поскольку амплитуды смещения диффузора с повышением частоты понижаются). Это позволяет увеличить, соответственно, уровень звукового давления в высокочастотной части АЧХ.
6. Снижение уровня нелинейных искажений, в частности, за счет эффекта Доплера (возникающих при модуляции высокочастотных составляющих низкочастотными компонентами сигнала).
Как правило, частоты среза в современных трехполосных акустических системах находятся в пределах: для низкочастотного громкоговорителя — 500…1000 Гц, для среднечастотного — от 500…1000 Гц до 5000…7000 Гц, для высокочастотного — 2000…5000 Гц.
Влияние на суммарные характеристики Анализ влияния разделительных фильтров на формирование суммарных АЧХ, ФЧХ и других характеристик акустических систем удобно производить на некоторой идеализированной модели, в которой предполагается, что громкоговорители имеют активное сопротивление и идеальные характеристики (плоская АЧХ, линейная ФЧХ, постоянный сдвиг фаз между излучателями и др.). При расчете фильтров необходимо предварительно выбрать частоту среза (как уже было показано ранее), порядок и тип фильтра (Баттерфорта, Чебышева, Линквитца-Риле или др.).
По получаемым суммарным характеристикам фильтры, обычно применяемые в акустических системах, можно разделить на три группы: фильтры линейно-фазовые (in-phase), фильтры всепропускающие-(all-pass) и все остальные.
Фильтры линейно-фазовые (in-phase) обеспечивают частотно-независимую суммарную АЧХ, линейную ФЧХ (точнее, равную нулю на всех частотах), а также равную нулю ГВЗ. Примером могут служить фильтры Баттерворта первого порядка. Суммарные характеристики для двухполосной системы с такими фильтрами показаны на рис. 6. Опыт их использования в акустических системах показал, что они обладают рядом недостатков: плохой избирательной способностью, большой неравномерностью характеристик мощности сигнала, плохой характеристикой направленности в полосе раздела и др. Поэтому в настоящее время они в акустических системах категории Hi-Fi не применяются.
Фильтры всепропускающие (all-pass) обеспечивают плоскую суммарную АЧХ, частотно-зависимые ФЧХ и ГВЗ. Требования к линейности ФЧХ является избыточным для акустических систем — достаточно, чтобы их ГВЗ были ниже порогов слышимости (как показывают результаты измерений, фильтры такого типа вносят искажения ГВЗ в полосе раздела, удовлетворяющие этим требованиям). К этому типу фильтров относятся фильтры Баттерворта нечетких порядков и фильтры Линквица-Риле четных порядков. При этом свойства фильтров реализуются при разной полярности включения каналов: для 2, 6, 10 порядков требуется включение каналов в противофазе, для 4, 8, 12 — нет. Для нечетных порядков: 1, 5, 9 должны включаться синфазно, 3,7… —противофазно. Суммарные и поканальные характеристики фильтров Линквица-Риле второго порядка и Баттерворта третьего порядка для двухканальной идеализированной акустической системы показаны на рис. 7 и рис. 8. Следует отметить (будет показано далее), что фильтры нечетких порядков создают поворот главного лепестка характеристики направленности в области частоты раздела.
Существует довольно большой класс фильтров, которые применяются в акустических системах, но они не относятся к «всепропускающему» типу. Сюда включаются фильтры второго и четвертого порядка Баттерворта, второго и четвертого порядка Бесселя, группа ассиметричных фильтров четвертого порядка Лежандра, Гаусса и др. Они не дают суммарную плоскую характеристику, но этот недостаток можно частично исправить, если сделать частоты среза между громкоговорителями несовпадающими. Например, на рис. 9а показаны характеристики фильтра Баттерворта четвертого порядка с пиком АЧХ в 3 дБ на частоте раздела, равной 1000 Гц. Если несколько разнести частоты, то есть сделать частоту раздела для НЧ 885 Гц, а для ВЧ 1138 Гц, то пик на АЧХ исчезает (рис. 9б).
Как уже было сказано, выбор типов фильтров для низко-, средне- и высокочастотного громкоговорителя кроме обеспечения плоской АЧХ в полосах раздела, определяется требованием к обеспечению симметричности характеристики направленностиакустической системы.
Внутри полосы пропускания каждого фильтра характеристика направленности акустической системы определяется характеристикой направленности каждого громкоговорителя, но внутри полосы раздела (полосы перекрытия фильтров) они работают совместно, то есть имеются два излучателя (например, средне и высокочастотный), которые разнесены в пространстве и работают на одной и той же частоте раздела. Пример такой системы показан на рис. 10. Пусть для простоты это будут два одинаковых излучателя, работающих в поршневом режиме с одинаковыми характеристиками направленности. На оси OA сигналы приходят в одинаковой фазе и складываются. Если оценить звуковое давление на оси OA’, где фазовый сдвиг за счет разности пути от одного и другого громкоговорителя составит φ=π (то есть 180 град), то сигналы будут складываться в противофазе и на характеристике направленности появится провал. При дальнейшем сдвиге от оси в точках, где разница фаз составит 2π (то есть 360 град), опять появится пик. В целом характеристика направленности будет иметь трехлепестковый характер (рис. 10).
Ширина главного лепестка характеристики направленности на частоте раздела зависит от отношения расстояния между громкоговорителями к длине волны, а наклон лепестка зависит от соотношения амплитуд и фаз разделяемых каналов, что определяется также и типом выбранных фильтров.
Для уменьшения этого явления надо стараться уменьшить расстояние между громкоговорителями (например, за счет применения коаксиальных громкоговорителей), уменьшить ширину полосы раздела (за счет выбора фильтров более высоких порядков) и, наконец, выбрать соответствующий тип фильтра, поскольку каждый фильтр вносит свои частотно-зависимые фазовые сдвиги.
Например, при использовании фильтров третьего порядка типа Баттерворта происходит поворот главного лепестка характеристики направленности вниз (при включении громкоговорителей в одинаковой фазе), рис. 11. При включении громкоговорителей в противофазе (то есть изменении их полярности) лепесток характеристики направленности смещается в другую сторону относительно оси.
Анализ фильтров различных типов и порядков показал, что фильтры четных порядков (всепропускающего типа) не изменяют симметричности направления лепестков, фильтры нечетных порядков поворачивают лепесток вниз или вверх. Симметричные характеристики направленности обеспечивают наибольшую равномерность излучаемой акустической мощности.
Помимо влияния на характеристику направленности по АЧХ фильтры могут оказывать влияние на фазочастотные характеристики и ГВЗ в полосе раздела. То есть характер переходных процессов, несмотря на симметрию АЧХ, может отличаться при одинаковых углах смещения в верхней и нижней полуплоскости, и ГВЗ, будучи ниже порогов слышимости на оси, могут превосходить пороги слышимости в других точках пространства, тем самым ухудшая качество звучания.
Следует еще раз напомнить, что все сделанные выводы относятся только к случаю идеальных характеристик громкоговорителей. Учет реальных характеристик производится с помощью современных компьютерных программ.
Расчет пассивных акустических фильтров Приступая к расчету пассивных акустических фильтров, необходимо уже четко определиться с конфигурацией системы (количеством полос воспроизведения, типами головок громкоговорителей и их параметрами, видом оформления — корпуса), а также выбрать порядок и тип фильтров в зависимости от основных задач, которые должны решаться при проектировании акустической системы: плоская АЧХ, линейная ФЧХ, симметричная характеристика направленности и др.
Поскольку в настоящее время в акустических системах чаще всего применяются фильтры типа «всепропускающих» (all-pass) с плоской АЧХ, то приведем приближенный расчет такого типа фильтров (более точные расчеты выполняются компьютерными методами).
Сначала разделительные фильтры рассчитываются из условия, что они нагружены на чисто активное сопротивление и питаются от генератора напряжения с малым выходным сопротивлением. Затем принимаются меры для учета влияния комплексной частотно-зависимой нагрузки громкоговорителей.
Расчет начинается с определения порядка фильтров и расчета элементов фильтра-прототипа. Фильтром-прототипом называется фильтр лестничного типа, элементы которого нормированы относительно единичной частоты среза и единичной нагрузки. Затем рассчитывается фильтр нижних частот для реальной частоты среза и реальной нагрузки, а из него путем преобразования частоты находятся элементы фильтра верхних частот и полосового фильтра.
Нормированные значения элементов фильтров-прототипов с первого по шестой порядок приведены в таблице 1.
Значения этих элементов даны только для фильтров «всепропускающего» типа, для других типов фильтров значения элементов в таблице будут другими. Схема фильтра-прототипа шестого порядка представлена на рис. 12. Фильтры меньших порядков получаются путем отбрасывания соответствующих элементов α (начиная с больших).
Значения реальных параметров фильтров для заданного порядка, сопротивления нагрузки Rн (Ом) и частоты среза fi (Гц) определяются следующим образом.
1. Для фильтра нижних частот: — каждая индуктивность-прототип α1, α3, α5 (рис. 12) заменяется на реальную индуктивность по формуле L=αi Rн/2πf1,(1) где i=1,3,5, f1 — частота среза фильтра нижних частот; — каждая емкость-прототип α2, α4, α6 заменяется на реальную емкость по формуле C=αi /2πf1Rн,(2) где i=2,4,6.
2. Для фильтра верхних частот (расчет происходит наоборот): — каждая индуктивность-прототип α1, α3, α5 заменяется на реальную емкость C=1/2πf2Rнαi,(3) где i=1,3,5, f2 — частота среза фильтра верхних частот; — каждая емкость-прототип заменяется на реальную индуктивность L=Rн/2πf2αi,(4) где i=2,4,6.
3. Для полосового фильтра: — каждая индуктивность-прототип α1, α3, α5 заменяется на последовательный контур из реальных L- и C-элементов, рассчитываемых по формулам: L=αiRн/2π(f2-f1),(5) С=1/4π2f02L,(6) где — средняя частота полосового фильтра; — каждая емкость-элемент α2, α4, α6 заменяется на параллельный контур из реальных L- и C-элементов, рассчитываемым по формулам: С=αi/2π(f2-f1)Rн,(7) L=1/4π2f02C.(8)
Фильтр Низких Частот (ФНЧ) — он же интегратор:
ФНЧ — фильтр, пропускающий без изменения частоты ниже частоты среза (f0) и подавляющий частоты выше f0. На частоте среза имеет значение амплитуды в -3dB. Это фильтр первого порядка и крутизна среза составляет 6дБ/октаву. Чаще всего такие фильтры используются для отсечения высокочастотных помех и шумов.
Октавой называется такой интервал частот, у которого конечное значение частоты больше начального в два раза.
Фильтр Высоких Частот (ФВЧ) — он же дифференциатор
ФВЧ — фильтр, ослабляющий частоты ниже частоты среза(f0) и пропускающий без изменения частоты выше f0. Так же как и у приведенного выше ФНЧ, сигнал на частоте среза обладает амплитудой в -3дБ, а крутизна среза 6 дБ на октаву.
И ФНЧ и ФВЧ работают как делитель напряжения, в котором одно плечо представлено постоянным резистором, а второе конденсатором, имеющим частотную зависимость.
Такие фильтры часто применяются на выходах звуковых усилителей для отсечения инфранизких, которые могут повредить АС.
Радиолюбитель
Практический расчет фильтров верхних и нижних частот (RC и LC фильтров)
Доброго дня уважаемые радиолюбители! Сегодня, на сайте “Радиолюбитель”, на очередном занятии “Практикума начинающего радиолюбителя”, мы с вами рассмотрим порядок расчета фильтров верхних и нижних частот.
Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).
В первую очередь определимся, что понятия
“верхние” и “нижние” частоты относятся к звукотехнике, а понятия “высокие” и “низкие” частоты – относятся к радиотехнике.
Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и служат для разных целей. Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный.
Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ). Что это за показатель.
АЧХ фильтра показывает как изменяется уровень амплитуду сигнала проходящего через этот фильтр в зависимости от частоты сигнала. Т.е., на одной частоте входящего на фильтр сигнала уровень амплитуды такой-же как и на выходе, а для другой частоты, фильтр, оказывая сопротивление сигналу, ослабляет амплитуду входящего сигнала.
Тут же появляется еще одно определение: частота среза.
Частота среза – это частота, на которой происходит спад амплитуды выходного сигнала до значения равного 0,7 от входного. Например, если при частоте входного сигнала 1 кГц амплитудой 1 вольт на выходе фильтра амплитуда входного сигнала уменьшается до 0,7 вольта, то частота 1 кГц является частотой среза данного фильтра.
И последнее определение – крутизна частотной характеристики фильтра.
Крутизна частотной характеристики фильтра – это показатель того, на сколько резко изменяется амплитуда входного сигнала на выходе при изменении его частоты. Чем быстрее происходит спад АЧХ тем лучше.
Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах.
Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала. Такое сопротивление называется реактивным и обозначается как Х.
Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:
Xc=1/2пFС где: Хс – реактивное сопротивление конденсатора; п – оно и в Африке “пи”; F – частота; С – емкость конденсатора. То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.
А реактивное сопротивление катушки индуктивности вот этой формулой:
XL=2пFL где: XL – реактивное сопротивление катушки индуктивности; п – оно и в России “пи”; F – частота сигнала; L – индуктивность катушки
Частотные фильтры бывают нескольких типов: – одноэлементные; – Г- образные; – Т – образные; – П – образные; – многозвенные.
В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов (фильтры с катушками индуктивности трогать не будем).
Одноэлементный фильтр
— фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот).
Г – образный фильтр
Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:
С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня. Формулы для расчета параметров делителя напряжения:
Uвх=Uвых*(R1+R2)/R2 Uвых=Uвх*R2/(R1+R2) Rобщ=R1+R2 R1=Uвх*R2/Uвых – R2 R2=Uвых*Rобщ/Uвх
К примеру, нам дано: Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 В Порядок расчета: 1. Определяем R2= 7*10000/10= 7000= 7 кОм 2. Определяем R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм 3. Проверяем Uвых=10*7000/(3000+7000)= 7 В Что нам и требовалось. Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже.
ВАЖНО! Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз. Это правило также справедливо и при расчетах фильтров.
Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор. Как вы уже знаете, конденсатор обладает реактивным сопротивлением. При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально.
При замене сопротивления R1 на конденсатор (при этом на высоких частотах ток через него проходит беспрепятственно, а на низких ток через него не проходит) мы получим фильтр верхних частот. А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот.
Как я уже сказал, уважаемые радиолюбители, мы не будем глубоко нырять в дебри электротехники, иначе мы заблудимся и забудем о чем шла речь. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему. Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей.
Порядок расчета Г-образного фильтра верхней частоты
В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен. А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.
Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц. Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).Проводим расчет: 1. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1. 2. Определяем по формуле делителя напряжения сопротивление R2: R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм. 3. Определяем сопротивление резистора R1: R1=Rобщ-R2= 5 – 3,5= 1,5 кОм. 4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях: Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7. 5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 —> C=1/2пFR1: C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ. Емкость конденсатора также можно определить по формуле: C=1,16/R2пF. 6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной: Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц. Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ. ? Для справки: ? 1 мкФ = 10-6 Ф = 0,000 001 Ф ? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф ? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф и так далее…
Порядок расчета Г-образного фильтра нижней частоты
Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.
Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц. Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).Проводим расчет: 1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2. 2. Определяем по формуле делителя напряжения сопротивление R2: R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм. 3. Определяем сопротивление резистора R1: R1=Rобщ-R2= 5 – 3,5= 1,5 кОм. 4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях: Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7. 5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 —> C=1/2пFR2: C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ. Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF. 6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной: Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц. Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.
Т – образный фильтр
Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:
П – образный фильтр
П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных. Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.
Для написания статьи, кроме всего прочего использовались материалы с сайта www.meanders.ru, автором и владельцем которого является Александр Мельник, за что ему большое и бесконечное (меандровское) спасибо.