ВВЕДЕНИЕ
В наше время высоких технологий всё более распространёнными становятся нелинейные нагрузки (частотные преобразователи, инверторы, системы бесперебойного питания, импульсные источники питания, люминесцентные и светодиодные лампы и т.п.). Из-за таких изменений в структуре нагрузки основной темой в этом десятилетии стали качество электроэнергии и снижение уровня гармоник. Проблемы, вызываемые гармониками, такие как перегрев трансформаторов и вращающихся машин, перегрузка проводников нейтрали, выход из строя конденсаторных батарей и т.п., приводят к повышению эксплуатационных расходов и также могут привести к снижению качества продукции и производительности труда. Кроме того, изменения в структуре генерации электроэнергии в сторону использования энергии ветра и солнечных батарей, которые тоже генерируют гармоники, также приводят к тому, что применение фильтров гармоник становится всё более важным для обеспечения стабильного энергоснабжения с приемлемым качеством электроэнергии.
Снизить уровень гармоник можно с использованием пассивных фильтров (составленных из конденсаторов, реакторов и резисторов) или активных фильтров (генерирующих гармоники в противофазе к гармоникам искажений и за счёт этого их уничтожающих)
Хотя основные принципы работы активных фильтров были выработаны ещё в 1970-е годы, они стали привлекать к себе повышенное внимание в последние несколько лет, потому что появилась возможность использования биполярных транзисторов с изолированным затвором (IGBT) и цифровых сигнальных процессоров (ЦСП). При этом разница в стоимости между активными и пассивными фильтрами становится не такой большой, как в прошлом
В этой статье сравниваются преимущества и недостатки активных и пассивных технологий фильтрации. Рассматриваются пассивные и активные решения для снижения уровня гармоник и стабилизации сети, направленные на решение проблем, которые возникают в современных областях применения и имеют тенденцию к возникновению в будущем.
Влияние фильтра на ФЧХ
Влияние фильтра на фазовую характеристику сигнала не менее значимо, чем его влияние на АЧХ. Для звуковых сигналов влияние ФЧХ фильтра на сигнал может оказаться решающим при выборе типа фильтра.
Не считая активного элемента (транзистора или микросхемы), активные фильтры, обычно, строятся на RC цепях. Каждая RC цепь — это полюс фильтра, перегибающий АЧХ в нужном нам направлении. Но одновременно с этим, каждая RC — цепь вносить конечную временную задержку в сигнал.
Такая задержка приводит к тому, что сигнал после фильтра будет сдвинут по фазе относительно исходного сигнала. Вся проблема заключается в том, что эта задержка может быть различна для разных частот.
Это касается любого фильтра. Но разница между типами фильтров в том, что они имеют разную фазово-частотную характеристику и разную крутизну среза.
Электромагнитная совместимость частотных преобразователей
Электромагнитная совместимость технических средств — это нормальная (с требуемым качеством) работоспособность технического оборудования в реальной окружающей обстановке несмотря на непреднамеренное воздействие электромагнитных помех и способность не создавать недопустимых помех другой технике.
Все модели векторных преобразователей частоты оснащаются сетевыми фильтрами, чем обеспечивается необходимый уровень ЭМС. Фильтры допускается не применять в диапазоне до 30 кВт. Все преобразователи частоты большей мощности снабжаются встроенными фильтрами по умолчанию. Встроенный фильтр даёт возможность доводить до минимума наводки и помехи в электронной технике.
Частота раздела
Тут самое время задуматься о частоте раздела. Обычно частота раздела выбирается на ровных горизонтальных участках, вдали от резонансов и завалов, стараясь обойти внезапные неравномерности как потенциальные источники искажений… А если вспомнить что существует фаза, о которой мало известно, а если известно, то векторно ачх на бумажке не сложишь, а из-за кривизны фаз даже на идеально ровной ачх что-то вылезет, что-то провалится в большей или меньшей степени. Также надо помнить что может дать сам динамик, особенно ВЧ, скажем не надо заставлять дюймовый купольник играть от двух, а тем более одного килогерца, даже если он способен их отыграть по АЧХ.
Итак, смотрим какие уникальные динамики нам достались. Высокочастотник начинает валить с 1,3 кгц, значит ниже его пускать нельзя. С другой стороны низкочастотник пытается играть по самые 10 кгц, с переменным успехом. Однако здравый смысл подсказывает, что выше килогерца его пускать плохая затея. И что спрашивается делать, если рабочие диапазоны динамиков не пересекаются?
Тут есть два варианта: если спады имеют адекватную крутизну, то лучше всего сводить в ямку, особенно если ямка получается широкой. В случае же нашем, когда спады круты как обрывы, надо держатся подальше от самого крутого из них. Чаще всего это может случится с высокочастотником, им всегда тяжко работать у нижней границы диапазона, поэтому им целесообразнее облегчить жизнь возлагая воспроизведение нижней части диапазона на НЧ динамик, который отыграет хоть плохо, но не нагадит. Поэтому ограничиваем диапазон участком от 1,5 кгц до 2,2 кгц.
Фазировка динамиков
На этом сведение подходит в концу. Остается только определиться с фазировкой динамиков. Тут есть как минимум три способа: на слух, по форме АЧХ и по фазовому сдвигу на частоте раздела. Если у динамиков АЧХ и ФЧХ в меру линейная, и фильтр фазу на разделе сильно не накручивает, то при смене правильной фазы на неправильную на частоте раздела появится глубокий провал, пропустить его сложно. В таком случае стоит подгонять фазу по по ее сдвигу. Сделать это можно осциллографом подавая на горизонтальную развертку сигнал с усилителя, а на вертикальное отклонение с микрофона.
Подают на вход усилителя синус с частотой раздела и не меняя взаимного расположения микрофона и колонки переключают ВЧ и НЧ динамики. По одинаковости фигур Лиссажу делается вывод о равенстве фаз излучателей. Этот метод хорошо подходит для фильтров первого порядка. С кривизной наших динамиков этот метод себя не оправдывает, поэтому сравниваем АЧХ при разной фазировке.
Второй вариант заметно хуже. Однако и первый не предел мечтаний, но так как двигать индуктивности катушек не просто, а ковыряться дальше уже лень, то все было оставлено как есть.
Порядок фильтра
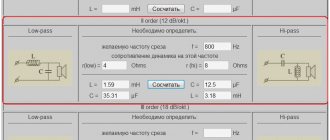
Обычно, когда встает вопрос о создании фильтра, первым делом необходимо определиться с тем, какая нужна крутизна спада. Она напрямую определяет порядок фильтра. Чем выше порядок ФНЧ, тем круче будет спад частотной характеристики выше частоты среза.
Для удобства, на этом и последующих графиках приводится нормированная частота. Т.е. как если бы все частоты были поделены на частоту среза фильтра.
Но чем выше порядок фильтра — тем сложнее он будет в реализации и капризнее в настройке. При этом, чем выше порядок, тем худшее воздействие он будет оказывать на частотные и/или фазовые характеристики сигнала.
Обычно, когда нужен фильтр высокого порядка, для упрощения схемотехники и расчетов, прибегают к последовательному включению двух, трех и более фильтров второго порядка. Это конечно облегчает задачу, но при таком включении требуется либо разные коэффициенты усиления каждого фильтра, либо разные частоты среза. Но это уже выходит за рамки данной статьи.
Расчет амплитудно-частотной характеристики фильтра
Мы можем рассчитать теоретическое поведение фильтра нижних частот, используя частотно-зависимую версию типового расчета делителя напряжения. Выходное напряжение резистивного делителя напряжения выражается следующим образом:
Рисунок 9 – Резистивный делитель напряжения
\
RC фильтр использует эквивалентную структуру, но вместо R2 у нас конденсатор. Сначала мы заменим R2 (в числителе) на реактивное сопротивление конденсатора (XC). Далее нам нужно рассчитать величину полного сопротивления и поместить его в знаменатель. Таким образом, мы имеем
\
Реактивное сопротивление конденсатора указывает величину противодействия протеканию тока, но, в отличие от активного сопротивления, величина противодействия зависит от частоты сигнала, проходящего через конденсатор. Таким образом, мы должны рассчитать реактивное сопротивление на определенной частоте, и формула, которую мы используем для этого, следующая:
\
В приведенном выше примере схемы R ≈ 160 Ом, и C = 10 нФ. Предположим, что амплитуда Vвх равна 1 В, поэтому мы можем просто удалить Vвх из расчетов. Сначала давайте рассчитаем амплитуду Vвых на частоте необходимой нам синусоиды:
\
\
Амплитуда необходимого нам синусоидального сигнала практически не изменяется. Это хорошо, поскольку мы намеревались сохранить синусоидальный сигнал при подавлении шума. Этот результат неудивителен, поскольку мы выбрали частоту среза (100 кГц), которая намного выше частоты синусоидального сигнала (5 кГц).
Теперь посмотрим, насколько успешно фильтр ослабит шумовую составляющую.
\
\
Амплитуда шума составляет всего около 20% от первоначального значения.
Классификация фильтров по виду их амплитудно-частотных характеристик
Фильтры нижних частот. Для фильтров нижних частот (ФНЧ) характерно то, что входные сигналы низких частот, начиная с постоянных сигналов, передаются на выход, а сигналы высоких частот задерживаются. На рис. 12.1,а
показана характеристика идеального (не реализуемого на практике) фильтра (ее иногда называют характеристикой типа «кирпичная стена»). На других рисунках представлены характеристики реальных фильтров.
Рис. 12.1.Амплитудно-частотные характеристики
фильтров нижних частот
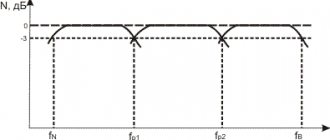
Полоса пропускания лежит в пределах от нулевой частоты до частоты среза ωс
. Обычно частоту среза определяют как частоту, на которой величина А(
ω
) равна 0,707 от максимального значения (т. е. меньше максимального значения на 3
дБ
).
Полоса задерживания (подавления) начинается от частоты задерживания ωз
и продолжается до бесконечности. В ряде случаев частоту задерживания определяют как частоту, на которой величина А(
ω
) меньше максимального значения на 40
дБ
(т. е. меньше в 100 раз).
Между полосами пропускания и задерживания у реальных фильтров расположена переходная полоса. У идеального фильтра переходная частота отсутствует.
Фильтры верхних частот. Фильтр верхних частот характерен тем, что он пропускает сигналы верхних и задерживает сигналы нижних частот.
На рис. 12.2,а
приведена идеальная (нереализуемая) амплитудно-частотная характеристика фильтра нижних частот, а на рис. 12.2,
б
– одна из типичных реальных. Через
ωс
и
ωз
обозначены частоты среза и задерживания.
Рис. 12.2. Амплитудно-частотные характеристики
фильтров верхних частот
Полосовые фильтры (полосно-пропускающие). Полосовой фильтр пропускает сигналы одной полосы частот, расположенной в некоторой внутренней части оси частот. Сигналы с частотами вне этой полосы фильтр задерживает.
На рис. 12.3,а
приведена амплитудно-частотная характеристика идеального (нереализуемого) фильтра и одна из типичных реальных характеристик (рис. 12.3,
б
). Через
ωс1
и
ωс2
обозначены две частоты среза,
ω0
– средняя частота. Она определяется выражением
.
Рис. 12.3. Амплитудно-частотные характеристики полосового фильтра
а-
идеальная характеристика;
б-
реальная характеристика
Режекторные фильтры (полосно-заграждающие). Режекторные фильтры не пропускают (задерживают) сигналы, лежащие в некоторой полосе частот, и пропускают сигналы с другими частотами.
Амплитудно-частотная характеристика идеального (нереализуемого) фильтра приведена на рис. 12.4,а
. На рис. 12.4,
б
показана одна из типичных реальных характеристик.
Рис. 12.4. Амплитудно-частотные характеристики
режекторного фильтра
Всепропускающие фильтры (фазовые корректоры). Эти фильтры пропускают сигналы любой частоты. Такие фильтры используются в некоторых электронных системах для того, чтобы изменить с той или иной целью фазочастотную характеристику всей системы (рис. 12.5).
Рис. 12.5. Амплитудно-частотная характеристика
всепропускающего фильтра
Классификация фильтров по передаточным функциям на примере фильтров низкой частоты. На практике широко используются фильтры, отличающиеся характерными особенностями амплитудно-частотных характеристик. Это фильтры Баттерворта, Чебышева, Бесселя (Томсона) (рис. 12.6).
Рис. 12.6. Амплитудно-частотные характеристики фильтров
Фильтры Баттерворта характеризуются наиболее плоской амплитудно-частотной характеристикой в полосе пропускания. Это их достоинство. Но в переходной полосе указанные характеристики спадают плавно, недостаточно резко.
Фильтры Чебышева отличаются резким спадом амплитудно-частотных характеристик в переходной полосе, но в полосе пропускания эти характеристики не являются плоскими.
Фильтры Бесселя характеризуются очень пологим участками амплитудно-частотных характеристик в переходной полосе, еще более пологими, чем у фильтров Баттерворта. Их фазочастотные характеристики достаточно близки к идеальным, соответствующим постоянному времени замедления, поэтому такие фильтры мало искажают форму входного сигнала, содержащего несколько гармоник.
Фильтры нижних частот. Для фильтров нижних частот (ФНЧ) характерно то, что входные сигналы низких частот, начиная с постоянных сигналов, передаются на выход, а сигналы высоких частот задерживаются. На рис. 12.1,а
показана характеристика идеального (не реализуемого на практике) фильтра (ее иногда называют характеристикой типа «кирпичная стена»). На других рисунках представлены характеристики реальных фильтров.
Рис. 12.1.Амплитудно-частотные характеристики
фильтров нижних частот
Полоса пропускания лежит в пределах от нулевой частоты до частоты среза ωс
. Обычно частоту среза определяют как частоту, на которой величина А(
ω
) равна 0,707 от максимального значения (т. е. меньше максимального значения на 3
дБ
).
Полоса задерживания (подавления) начинается от частоты задерживания ωз
и продолжается до бесконечности. В ряде случаев частоту задерживания определяют как частоту, на которой величина А(
ω
) меньше максимального значения на 40
дБ
(т. е. меньше в 100 раз).
Между полосами пропускания и задерживания у реальных фильтров расположена переходная полоса. У идеального фильтра переходная частота отсутствует.
Фильтры верхних частот. Фильтр верхних частот характерен тем, что он пропускает сигналы верхних и задерживает сигналы нижних частот.
На рис. 12.2,а
приведена идеальная (нереализуемая) амплитудно-частотная характеристика фильтра нижних частот, а на рис. 12.2,
б
– одна из типичных реальных. Через
ωс
и
ωз
обозначены частоты среза и задерживания.
Рис. 12.2. Амплитудно-частотные характеристики
фильтров верхних частот
Полосовые фильтры (полосно-пропускающие). Полосовой фильтр пропускает сигналы одной полосы частот, расположенной в некоторой внутренней части оси частот. Сигналы с частотами вне этой полосы фильтр задерживает.
На рис. 12.3,а
приведена амплитудно-частотная характеристика идеального (нереализуемого) фильтра и одна из типичных реальных характеристик (рис. 12.3,
б
). Через
ωс1
и
ωс2
обозначены две частоты среза,
ω0
– средняя частота. Она определяется выражением
.
Рис. 12.3. Амплитудно-частотные характеристики полосового фильтра
а-
идеальная характеристика;
б-
реальная характеристика
Режекторные фильтры (полосно-заграждающие). Режекторные фильтры не пропускают (задерживают) сигналы, лежащие в некоторой полосе частот, и пропускают сигналы с другими частотами.
Амплитудно-частотная характеристика идеального (нереализуемого) фильтра приведена на рис. 12.4,а
. На рис. 12.4,
б
показана одна из типичных реальных характеристик.
Рис. 12.4. Амплитудно-частотные характеристики
режекторного фильтра
Всепропускающие фильтры (фазовые корректоры). Эти фильтры пропускают сигналы любой частоты. Такие фильтры используются в некоторых электронных системах для того, чтобы изменить с той или иной целью фазочастотную характеристику всей системы (рис. 12.5).
Рис. 12.5. Амплитудно-частотная характеристика
всепропускающего фильтра
Классификация фильтров по передаточным функциям на примере фильтров низкой частоты. На практике широко используются фильтры, отличающиеся характерными особенностями амплитудно-частотных характеристик. Это фильтры Баттерворта, Чебышева, Бесселя (Томсона) (рис. 12.6).
Рис. 12.6. Амплитудно-частотные характеристики фильтров
Фильтры Баттерворта характеризуются наиболее плоской амплитудно-частотной характеристикой в полосе пропускания. Это их достоинство. Но в переходной полосе указанные характеристики спадают плавно, недостаточно резко.
Фильтры Чебышева отличаются резким спадом амплитудно-частотных характеристик в переходной полосе, но в полосе пропускания эти характеристики не являются плоскими.
Фильтры Бесселя характеризуются очень пологим участками амплитудно-частотных характеристик в переходной полосе, еще более пологими, чем у фильтров Баттерворта. Их фазочастотные характеристики достаточно близки к идеальным, соответствующим постоянному времени замедления, поэтому такие фильтры мало искажают форму входного сигнала, содержащего несколько гармоник.
Полосовые резонансные фильтры
Полосовые резонансные частотные фильтры – предназначены для выделения, или режекции (вырезания) определённой полосы частот. Резонансные частотные фильтры могут состоять из одного, двух, или трех колебательных контуров, настроенных на определённую частоту. Резонансные фильтры обладают наиболее крутым подъёмом (или спадом) АЧХ, по сравнению с другими (не резонансными) фильтрами. Полосовые резонансные частотные фильтры могут быть одноэлементными — с одним контуром, Г-образными – с двумя контурами, Т и П-образными – с тремя контурами, многозвенными – с четырьмя и более контурами.
На рисунке представлена схема Т-образного полосового резонансного фильтра, предназначенного для выделения определённой частоты. Состоит он из трёх колебательных контуров. CL
и
CL
– последовательные колебательные контуры, на резонансной частоте имеют малое сопротивление протекающему току, а на других частотах наоборот – большое. Параллельный контур
CL
наоборот, имеет большое сопротивление на резонансной частоте, обладая малым сопротивлением на других частотах. Для расширения ширины полосы пропускания такого фильтра, уменьшают добротность контуров, изменяя конструкцию катушек индуктивности, расстраивая контура «вправо, влево» на частоту, немного отличающуюся от центральной резонансной, параллельно контуру
CL
подключают резистор.
На следующем рисунке представлена схема Т-образного режекторного резонансного фильтра, предназначенного для подавления определённой частоты. Он, как и предыдущий фильтр состоит из трёх колебательных контуров, но принцип выделения частот у такого фильтра другой. CL
и
CL
– параллельные колебательные контуры, на резонансной частоте имеют большое сопротивление протекающему току, а на других частотах – маленькое. Параллельный контур
CL
наоборот, имеет малое сопротивление на резонансной частоте, обладая большим сопротивлением на других частотах. Таким образом, если предыдущий фильтр резонансную частоту выделяет, а остальные частоты подавляет, то этот фильтр, беспрепятственно пропускает все частоты, кроме резонансной частоты.
Порядок расчёта полосовых резонансных фильтров основан всё на том же делителе напряжения, где в качестве единичного элемента выступает LC контур с его характеристическим сопротивлением. Как рассчитывается колебательный контур, определяются его резонансная частота, добротность и характеристическое (волновое) сопротивление вы можете найти в статье Колебательный контур.
Фильтра Чебышева и звук?
Начнем с фильтра Чебышева. Он имеет самый резкий спад частотной характеристики. Но вносимый им фазовый сдвиг сильно меняется во всей полосе пропускания. По этой причине фильтр Чебышева не применяется в высококачественных звуковых цепях.
Но это не единственный минус. Фильтра Чебышева так же имеет и большую неравномерность АЧХ в полосе пропускания. При этом сумма максимумов и минимумов равна порядку фильтра
На следующем графике приведены амплитудно-частотные (левая шкала) и фазово-частотные (правая шкала) характеристики для фильтра Чебышева 8-го порядка. Все тоже самое свойственно и фильтрам Чебышева более низких порядков.
Звучание системы
И конечно же надо сказать про звук. Стало лучше, сцена получилась очень недурственная. Кривизна АЧХ особо не слышна, даже наоборот, подъем на середине поддает детальности, верхов как ни странно хватает. Был замечен интересный эффект на басу. Как можно заметить по АЧХ на сотне герц большой подъем, а за ним завал, разумеется качающего баса нет, но есть мид бас. К примеру партия гитары кажется немного просаженным, а нижний бас, партия бас гитары, переходит как бы в слышимую область и читается очень четко, создается впечатление наличия того самого низкого баса.
Конечно ящики маловаты, и порой слышно подбубнивание, для устранения этого эффекта в каждую колонку было добавлено по 30 грамм натуральней шерсти. В целом данная акустика играет тепло и мягко даже без лампового усилителя, сохраняя в звуке строгость и точность камня, а вот с теплой лампой получается перебор мягкости. Все же им нужен усилитель по-строже — триод или двухтакт, но это тема для следующих экспериментов. Специально для сайта Радиосхемы — SecreTUseR.
Обсудить статью ФИЛЬТР ДЛЯ АКУСТИКИ
Практическая работа
Плавно переходим от теории к практике. Достались мне винтажные колонки под названием Kompaktbox B 9251. И первое что было сделано — произведено прослушивание.
С холодным камнем звук был в среднем не плох, а если говорить конкретно, то местами хороший, а местами как попало. С теплой лампой играть вообще отказались. На основе этих наблюдений был сделан вывод о наличии глубоко зарытого потенциала. Вскрытие показало, что немецкие инженеры решили обойтись одним единственным конденсатором последовательно с ВЧ головкой. Измерение АЧХ дало страшную картину
На рисунке АЧХ одной колонки, кривая с глубокой дыркой на 6 кгц из-за плохого контакта разъема, на нее внимание не обращать. АЧХ отдельно ВЧ и НЧ приведены ниже
Т — образные фильтры высоких и низких частот
Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза. Преобразование фильтров показано на рисунках. Особенность Т-образных фильтров заключается в том, что они по сравнению с Г-образными, своим выходным сопротивлением оказывают меньшее шунтирующее действие на радио цепи, стоящие за фильтром.
Преобразование Г-образного RC фильтра высоких частот, в Т-образный RC фильтр высоких частотПреобразование Г-образного RC фильтра низких частот, в Т-образный RC фильтр низких частотПреобразование Г-образного RL фильтра высоких частот, в Т-образный RL фильтр высоких частотПреобразование Г-образного RL фильтра низких частот, в Т-образный RL фильтр низких частотПреобразование Г-образного LС фильтра высоких частот, в Т-образный LС фильтр высоких частотПреобразование Г-образного LС фильтра низких частот, в Т-образный LС фильтр низких частот
П – образный фильтр
П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных. Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.
Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.
А.И.Шихатов 2003
Традиционно раздел полос СЧ и ВЧ (или мидбас-ВЧ) производят пассивными кроссоверами (разделительными фильтрами). Это особенно удобно при использовании готовых компонентных наборов. Однако, хотя характеристики кроссоверов и оптимизированы для данного комплекта, они не всегда удовлетворяют поставленной задаче. Рост индуктивности звуковой катушки с частотой приводит к увеличению импеданса головки. Причем индуктивность эта у «среднестатистического» мидбаса составляет 0,3-0,5 мГн, и уже на частотах 2-3 кГц импеданс возрастает практически в два раза. Поэтому при расчете пассивных кроссоверов применяют два подхода: используют в расчетах реальное значение импеданса на частоте раздела или вводят цепи стабилизации импеданса (компенсаторы Цобеля). Об этом уже написано немало, поэтом не будем повторяться. У пищалок стабилизирующие цепи обычно отсутствуют. При этом исходят из того, что рабочая полоса частот невелика (две-три октавы), а индуктивность незначительна (обычно менее 0,1 мГн). Вследствие этого рост импеданса невелик. В крайнем случае, увеличение импеданса компенсируют резистором сопротивлением 5-10 Ом, включенным параллельно пищалке. Однако все не так просто, как кажется на первый взгляд, и даже такая скромная индуктивность приводит к любопытным последствиям. Проблема заключена в том, что пищалки работают совместно с фильтром ВЧ. Независимо от порядка в нем имеется емкость, включенная последовательно с пищалкой, и она образует с индуктивностью звуковой катушки колебательный контур. Частота резонанса контура оказывается в полосе рабочих частот пищалки, и на АЧХ возникает «горб», величина которого зависит от добротности этого контура. В результате неизбежна окраска звучания. В последнее время появилась немало моделей пищалок высокой чувствительности (92 дБ и выше), индуктивность которых достигает 0,25 мГн. Поэтому вопрос согласования пищалки с пассивным кроссовером приобретает особую остроту. Для анализа использовалась среда моделирования Micro-Cap 6.0, но те же результаты можно получить и с помощью других программ (Electronic WorkBench, например). В качестве иллюстраций приведены только наиболее характерные случаи, остальные рекомендации даны в конце статьи в виде выводов. В расчетах использовалась упрощенная модель пищалки, учитывающая только ее индуктивность и активное сопротивление. Данное упрощение вполне допустимо, поскольку резонансный пик импеданса большинства современных пищалок невелик, а частота механического резонанса подвижной системы находится за пределами рабочей полосы частот. Учтем также, что АЧХ по звуковому давлению и АЧХ по электрическому напряжению — две большие разницы, как говорят в Одессе. Взаимодействие пищалки с кроссовером особенно хорошо заметно у фильтров первого порядка, характерных для недорогих моделей (рисунок 1):
Рисунок 1
Видно, что даже при индуктивности 0,1 мГн имеется выраженный пик в области частот 7-10 кГц, придающий звучанию характерную «хрустальную» окраску». Увеличение индуктивности смещает резонансный пик в область более низких частот и увеличивает его добротность, что приводит к заметному «цыканью». Побочное следствие увеличение добротности, которое можно обратить на пользу — увеличение крутизны АЧХ. В области частоты раздела она близка к фильтрам 2 порядка, хотя на большом удалении возвращается к исходному для 1 порядка значению (6 дБ/октава). Введение шунтирующего резистора позволяет «приручить» горб на АЧХ, так что на кроссовер можно возложить и некоторые функции эквалайзера. Если шунт сделать на основе переменного резистора (или набора резисторов с переключателем), то можно проводить даже оперативную регулировку АЧХ в пределах 6-10 дБ. (рисунок 2):
Рисунок 2
Однако фильтры первого порядка обеспечивают слишком малое затухание за пределами рабочей полосы, поэтому пригодны только при небольшой подводимой мощности или достаточно высокой частоте раздела (7-10 кГц). Поэтому в большинстве серьезных конструкций используют фильтры более высоких порядков, от второго до четвертого. Рассмотрим возможности воздействия на АЧХ для фильтров второго порядка, как самых распространенных. Для наглядности использована модель с большой индуктивностью. Те же результаты получаются и с традиционными пищалками, только параметры фильтров и степень воздействия на АЧХ будут другими. Для пищалок с малой индуктивностью шунт не обязателен. Первый способ — изменение добротности фильтра при неизменной частоте раздела за счет соотношения емкости и индуктивности фильтра (рисунок 3):
Рисунок 3
Одновременное изменение емкости и индуктивности в кроссовере затруднено, поэтому данный метод для оперативной регулировки неудобен. Однако он незаменим в тех случаях, когда необходимая степень коррекции известна заранее, на этапе проектирования.
Второй способ — регулировка добротности при помощи шунта (аналогично рассмотренному ранее способу для фильтра первого порядка). Исходная добротность разделительного фильтра при этом выбирается высокой (рисунок 4):
Рисунок 4
Третий способ — введение резистора последовательно с пищалкой. Особенно удобен этот способ для пищалок индуктивностью свыше 100 мГн. В этом случае суммарный импеданс цепи «резистор-пищалка» в процессе регулирования изменяется незначительно, поэтому уровень сигнала практически не изменяется (рисунок 5):
Рисунок 5
Выводы Стабилизирующие цепи не обязательны только для пищалок малой индуктивности (менее 0,05 мГн). Для пищалок с индуктивностью звуковой катушки 0,05-0,1 мГн наиболее выгодны параллельные стабилизирующие цепи (шунты). Для пищалок с индуктивностью звуковой катушки более 0,1 мГн можно использовать как параллельные, так и последовательные стабилизирующие цепи. Изменение сопротивления стабилизирующей цепи позволяет воздействовать на АЧХ. Для фильтров 1 порядка изменение параметров стабилизирующей цепи оказывает заметное влияние на частоту среза и параметры «горба». У фильтров 2 порядка частота среза определяется параметрами его элементов и зависит от индуктивности головки и параметров стабилизирующей цепи в меньшей степени. Величина резонансного «горба», вызванного индуктивностью пищалки, находится в прямой зависимости от сопротивления шунта и в обратной зависимости от сопротивления последовательного резистора. Величина резонансного «горба» в области частоты среза находится в прямой зависимости от добротности фильтра. Добротность фильтра пропорциональна результирующему сопротивлению нагрузки (ВЧ головки с учетом сопротивления стабилизирующей цепи). Фильтр повышенной добротности можно рассчитывать по стандартной методике, но на сниженное в 2-3 раза относительно номинального сопротивление нагрузки.
Предложенные способы регулирования АЧХ применимы и к фильтрам более высоких порядков, но, поскольку число «степеней свободы» там возрастает, дать конкретные рекомендации в этом случае затруднительно. Пример изменения АЧХ фильтра третьего порядка за счет шунтирующего резистора приведен на рисунке 6:
Рисунок 6
Видно, что АЧХ приобретает различный вид, что заметно влияет на тембр звучания. Кстати, лет 20 назад многие «домашние» трех-четырех полосные АС имели переключаемые АЧХ «normal/crystal/chirp» («гладкий-хрустальный-чирикающий»). Это достигалось изменением уровня полос СЧ и ВЧ. Переключаемые аттенюаторы используются в составе многих кроссоверов, причем по отношению к пищалке их можно рассматривать как комбинацию последовательных и параллельных стабилизирующих цепей. Воздействие их на результирующую АЧХ предсказать достаточно сложно, в этом случае удобнее прибегнуть к моделированию.
Рисунок 7
На рисунке 7 приведена схема и АЧХ фильтра третьего порядка, разработанного автором для пищалок Prology RX-20s и EX-20s. В конструкции использованы конденсаторы К73-17 (2,2 мкФ, 63 В) и самодельные катушки индуктивности. Для снижения активного сопротивления они намотаны на ферритовых кольцах. Тип сердечника неизвестен: наружный диаметр 15 мм, магнитная проницаемость порядка 1000-2000. Поэтому подгонка индуктивности велась по прибору Ф-4320. Каждая катушка содержит 13 витков изолированного провода диаметром 1 мм. Качество звучания оказалось не в пример выше исходного, а регулирование АЧХ вполне соответствовало поставленной задаче. Однако следует отметить, что фильтр получился проблемным: входной импеданс имеет резко выраженный минимум, и возможно срабатывание защиты усилителя.
Адрес администрации сайта
НЕ НАШЕЛ, ЧТО ИСКАЛ? ПОГУГЛИ:
СТРОКА ПОЛЬЗОВАТЕЛЬСКОГО ПОИСКА
ПОСОБЫ СНИЖЕНИЯ УРОВНЯ ГАРМОНИК
Возможные способы ослабления гармоник – это, например, увеличение тока короткого замыкания сети (снижение импеданса сети), ограничение производительности / количества одновременно работающих источников гармоник, сбалансированное подключение однофазных нагрузок к трём фазам и применение оборудования с большей пульсностью (к примеру, использование 12– или 18-пульсного частотного преобразователя вместо 6-пульсного). Однако наиболее распространёнными решениями являются использование пассивного фильтра, состоящего из комбинации конденсаторов, индуктивностей и сопротивлений (RC, RL , LC, LCQ и других), а также получающих всё более широкое распространение активных фильтров. Также применяются гибридные решения (комбинации активных и пассивных фильтров).
При использовании пассивного резонансного фильтра его схема настраивается на определённую частоту, то есть резонансные частоты последовательного фильтра очень близки к частотам имеющихся гармоник. При проектировании резонансного фильтра большое значение имеет тщательный анализ нагрузки и качества электроэнергии, также очень важна величина импеданса сети (рисунок 2).
Рис. 2. Зависимость импеданса шинопровода системы от частоты
Как показано на рисунке 3, для резонансной фильтрации важна последовательность коммутации, она должна следовать правилу LIFO (последним пришёл – первым вышел), обратное может привести к проблемам.
Рис. 3. Последовательность коммутации резонансных фильтров в соответствии с правилом LIFO
А) Пример: применение резонансного фильтра
На приведённом ниже реальном примере (рисунки 4, 5) показан резонансный фильтр для 5-й и 7-й гармоник. Он установлен в торговом центре в Китае.
Рис. 4. Электрическая схема подключения резонансного фильтра в торговом центре в Китае
Результаты анализа фильтра показаны на рисунке 5. Можно увидеть, что не только уменьшены токи 5-й и 7-й гармоник, но также снизились гармонические искажения напряжения с 4,8% до 1,8%. Также увеличилось значение коэффициента мощности с 0,92 до 0,99.
| РЕЗОНАНСНЫЕ ФИЛЬТРЫ | Результат/уменьшение | |||||||||
| Без фильтра | 1 фильтр 5-й гармоники (1) вкл. | 2-й фильтр 5-й гармоники (2) вкл. | Фильтр 7-й гармоники (3) вкл. | |||||||
| 11:09:30 | 11:10:00 | 11:11:00 | 11:11:30 | |||||||
| Активная мощность, кВт | P | 1489 | 1494 | 1497 | 1506 | |||||
| Реактивная мощность, квар | Q | 641 | 364 | 188 | 190 | 70,36% | ||||
| Полная мощность, кВА | S | 1621 | 1538 | 1509 | 1518 | 6,35% | ||||
| Напряжение, В | U | 234 | 235,567 | 237,075 | 238,867 | 2,08% | ||||
| Действ. значение тока, А | Irms | 2266 | 2109 | 2050 | 2078 | 8,30% | ||||
| Коэффициент нелинейных искажений | THD-V | 4,78% | 3,04% | 2,79% | 1,78% | 62,82% | ||||
| Напряжение 5-й гармоники | HRU5 | 3,83% | 0,89% | 0,81% | 0,94% | 75,38% | ||||
| Напряжение 7-й гармоники | HRU7 | 1,77% | 2,32% | 2,15% | 0,89% | 49,49% | ||||
| Напряжение 11-й гармоники | HRU11 | 1,40% | 0,89% | 0,86% | 0,62% | 56,00% | ||||
| Коэффициент нелинейных искажений тока | THD-I | 17,68% | 394,51 A | 9,92% | 208,25 A | 9,93% | 202,51 A | 6,56% | 135,94 A | 65,54% |
| Ток 5-й гармоники | HRI5 | 16,21% | 361,71 A | 3,85% | 80,82 A | 4,31% | 87,90 A | 5,12% | 106,17 A | 70,65% |
| Ток 7-й гармоники | HRI7 | 4,68% | 104,43 A | 8,16% | 171,19 A | 7,99% | 163,03 A | 2,75% | 56,98 A | 45,44% |
| Ток 11-й гармоники | HRI11 | 3,38% | 75,47 A | 2,30% | 48,31 A | 1,87% | 38,23 A | 1,13% | 23,33 A | 69,09% |
| Ток основной частоты | I1 | 2231 | 2099 | 2040 | 2074 | 7,07% | ||||
| Коэффициент мощности | PF | 0,92 | 0,97 | 0,99 | 0,99 |
Рис. 5. Результаты применения резонансного фильтра в торговом центре в Китае
B) Преимущества и недостатки пассивных фильтров
Как собрать фильтр низких частот
Инструкция, как правильно сделать фильтр низких частот полезна для многих. В радиотехнике всегда требуется изготавливать фильтры разной высотности. И сделать самостоятельно фильтр низких частот не так уж сложно.
Вот, что нужно для изготовления фильтра низких частот:
- Разнообразные детали для припаиваня к печатной плате.
- Стеклотекстролит для печатной платы.
- Источник тока.
- Паяльник простой.
Далее распечатываем рисунок дорожек для платы и переносим его на нашу заготовку.
Если дорожки получаются не четкими, их следует дорисовать, используя лак. После того, как все перенесено, необходимо очистить плату при помощи специального раствора.
Создать раствор можно из лимонной кислоты и перекиси водорода. Их смешивают в пропорции 1:3 соответственно. Для более быстрого действия раствора туда добавляется катализатор — соль на кончике ножа.
Как только готов раствор, в него помещается плата и выжидается время до полной очистки. Медь, которая осталась на поверхности дорожек должна полностью раствориться. По окончании очистки платы необходимо ополоснуть ее под проточной водой.
По окончании процесса можно начать припаивать детали. Для того, чтобы сделать все точно, обратитесь к видео мастер-классу по припаиванию деталей.
Таким образом, вы заметили, насколько просто самостоятельно создать фильтр низких частот. По такому же принципу вы можете самостоятельно придумать схему изготовления и фильтра высокой частотности.
Активные кроссоверы для АС основе фильтра Баттерворта 3-го порядка
Всем привет, Чтобы не иметь сложностей с расчётом фильтра СЧ-ВЧ, возможно, представляется правильным, использовать, так называемый фильтр дополнительной функции (ФДФ) – дифференциальный усилитель, вычитающий из широкополосного (музыкального) сигнала тот, что был выделен фильтром низких частот (в нашем случае), а остаток – СЧ и ВЧ составляющие, передающий на свой выход.
Практические схемы кроссоверов с ФДФ подробно описаны в статьях журнала Радио: 1981г №5-6 стр 39 «Трёхполосный усилитель» 1987г №3 стр 35 «Блок фильтров трёхполосного усилителя ЗЧ»
Обратите внимание, в схеме ’87/3, перед активным фильтром стоит повторитель напряжения на ОУ, каковой повторитель обладает низким выходным сопротивлением, а нагружен фильтр на ОУ (ФДФ) с высоким входным сопротивлением, что полезно для согласования фильтра со схемой, образующей кроссовер, в целом.
Частоту раздела, для двухполосного кроссовера, лучше выбрать в три раза больше, чем резонансная частота НЧ громкоговорителя. Если в качестве НЧ громкоговорителя используется широкополосный динамик, то раздел лучше провести выше 3,5 КГц (выше резонансной частоты выбранного ВЧ динамика). Таблица с связывающая частоту раздела при биамплиннге с мощностью, которую нужно подвести к СЧ – ВЧ звену, приведена в Радио 2001 №9 стр. 10
Перед этим кроссовером, хорошо бы поставить ФВЧ с частотой среза 40Гц или менее – отрезать то, что Ваш НЧ динамик не может воспроизвести физически. Подробно об этом рассказано у Аудиокиллера electroclub.info/samodel/sub_pred.htm
Статья по измерению резонансной частоты громкоговорителей и их «Т-С параметров» при помощи звуковой карты компьютера, приведена здесь, на сайте. datagor.ru/practice/loudspeakers/1366-izmerenie-parametrov-tilya-smolla-dlya-nachinayushhix.html
По теме двухполосного звуковоспроизведения (биамплинг), интересно прочитать статью В.Шорова из Радио 1994 №2 «Двухполосное звуковоспроизведение» и, если есть желание разобраться лучше – цикл статей А.Фрунзе «О повышение качества звучания АС» Радио 1992 9 – 12.
Хочу поблагодарить АудиоКиллера за программу для расчёта фильтров третьего порядка. electroclub.info/mysoft.htm По выполненным расчётам собрал комбинированный (на одном ОУ) полосовой фильтр 40 – 18000 Гц для УКВ приёмника. При точном подборе конденсаторов и резисторов, АЧХ фильтра совпала с желаемой без дополнительной настройки.
Начинающие, успешно собравшие макет схемы, могут избавить себя от хлопот травления печатных плат, используя НЕфольгированный стеклотекстолит (гетинакс или плотный картон) и тонкий лужёный провод, который заменяет дорожки, которые предполагалось травить. В программе LayOut рисуется печатная плата, с шириной дорожек 0,3 – 05 мм. – чтобы были видны. По распечатке рисунка платы, защищённой прозрачным скотчем, кернится и сверлится текстолит. Потом в отверстия, по порядку сборки, от входа у выходу, вставляются детали, их лужёные выводы отгибаются по направлению отрисованных дорожек и пропаиваются. Если длинны выводов не хватает, используют лужёный провод. Если проводники — «дорожки» лежат близко друг к другу и есть риск замыкания – можно одеть кембрик. Важно, что если потребуется переделка, например, 20% собранной схемы, не нужно срезать печатные дорожки – просто распаять участок, сделать новую сверловку и собрать заново – чисто, просто и технологично, как тротуарная плитка. При сборке ВЧ конструкций, слой фольги, обращённый к деталям, можно использовать как общий экран. Фольгу вокруг отверстий нужно зенковать, кроме «земляных» контактов. Если интересно, пришлю фотографии плат, сделанных таким способом.
Влияние помех на приводное оборудование
В промышленности большая часть электропотребления приходится на вентиляторы, насосы, компрессоры, конвейеры и лебёдки, приводы технологических установок. Механическая часть всего этого хозяйства приводится в действие асинхронными двигателями переменного тока. Режимное управление работы асинхронных двигателей, включая сокращение потребления ими электроэнергии, осуществляется с помощью специализированных устройств – преобразователей частоты. Польза их заключается в значительном облегчении пусковых режимов и работы непосредственно асинхронных двигателей. Однако иногда частотные преобразователи оказывают и нежелательное влияние на двигатель.
В виду особенной конструкции преобразователя частоты, его напряжение и ток на выходе имеют форму всплеска с огромным числом помех. Выпрямитель преобразовательного устройства, потребляя нелинейный ток, создаёт высшие гармоники, тем самым загрязняя электрическую сеть. Инвертор частотного преобразователя (ШИМ) – генерирует широкий спектр высокочастотных гармоник.
Электропитание обмоток двигателя таким нестандартным током подчас доводит до теплового и электрического пробоя изоляции обмоток двигателя, износу изоляции, увеличению степени акустических шумов работающего мотора, эрозии подшипников. Помимо этого, частотные преобразователи источают помехи в электрической сети, что оказывает отрицательное воздействие на остальное электрооборудование, питающееся от этой же электросети. Для уменьшения неблагоприятного влияния гармонических искажений, создаваемых преобразователем частоты в процессе работы, на электросеть, для двигателя и самого преобразователя частоты используется фильтрация.
Одноэлементные фильтры высоких и низких частот
Как правило, одноэлементные фильтры высоких и низких частот применяют непосредственно в акустических системах мощных усилителей звуковой частоты, для улучшения звучания самих звуковых «колонок».
Они подключаются последовательно с динамическими головками. Во первых, они берегут как динамические головки от мощного электрического сигнала, так и усилитель от низкого сопротивления нагрузки не нагружая его лишними динамиками, на той частоте, которую эти динамики не воспроизводят. Во вторых, они делают воспроизведение приятнее на слух.
Чтобы рассчитать одноэлементный фильтр, необходимо знать реактивное сопротивление катушки динамической головки. Расчёт производится по формулам делителя напряжения, что так же справедливо для Г-образного фильтра. Чаще всего, одноэлементные фильтры подбирают «на слух». Для выделения высоких частот на «пищалке» последовательно с ней устанавливается конденсатор, а для выделения низких частот на низкочастотном динамике (или сабвуфере), последовательно с ним подключается дроссель (катушка индуктивности). Например, при мощностях порядка 20…50 Ватт, на пищалки оптимально использовать конденсатор на 5…20 мкФ, а в качестве дросселя низкочастотного динамика использовать катушку, намотанную медным эмалированным проводом, диаметром 0,3…1,0 мм на бобину от видеокассеты VHS, и содержащую 200…1000 витков. Указаны широкие пределы, потому, как подбор – дело индивидуальное.
Расчёт фильтров АС. Фазовый метод.
ФИЛЬТР —
устройство выделения желательных компонентов спектра сигнала и
подавление нежелательных.
Фазовый метод расчёта фильтров АС.
Требования потребителей к качеству воспроизведения звука часто зависит от выработанных склонностей индивида, но скорее всего их, эти требования можно классифицировать по степени востребованности однотипными по притязяниям группами людей, выделяя некоторое число основных параметров, предъявляемых к качеству. Параметры различны, но в первую очередь качество звука определяется шириной рабочего диапазона частот и величиной нелинейных и фазовых искажений. В частности, для воспроизведения низких, средних и высоких частот нашли широкое применение многополосные акустические системы (АС). Для разделения полос звукового спектра динамические головки включаются через разделительные фильтры первого, второго или более высокого порядка. Однако, как известно, точное разделение частот сложного звукового сигнала на граничной частоте раздела fp выполнить невозможно (рис. 1). Поэтому между соседними полосами воспроизведения динамических головок имеется зона совместного действия. Сигнал с частотой раздела fp обе головки воспроизводят с примерно равным уровнем. На других частотах зоны совместного действия уровни сигналов, подаваемых на головки, резко отличаются друг от друга по амплитуде. Для идеального воспроизведения звука в зоне совместного действия должны быть обеспечены условия для синфазной по звуковому давлению работы обеих головок, т. е. между токами головок не должно быть фазового сдвига, а зона совместного действия должна быть как можно меньше. Однако выполнить эти условия весьма затруднительно.
Фильтры первого порядка (рис. 1, а) просты, их амплитудночастотные характеристики (АЧХ) имеют пологую форму, и благодаря этому зоны совместного действия динамических головок относительно, широки. Например, зона совместного действия низкочастотной ВА1 и среднечастотной ВА2 головок примерно равна 50… 5000 Гц (рис. 1, б).
Рис. 1. Простые разделительные фильтры:
а — принципиальные схемы; б — амплитудночастотные характеристики; в — фазочастотные характеристики
Для АС, содержащих три динамические головки, могут быть зоны одновременного действия всех трех головок (рис. 1, б, 500…5000 Гц). ( Амплитудночастотные характеристики строились до уровня сигналов практической слышимости звучания динамических головок.)
В таких разделительных фильтрах последовательно с низкочастотной (НЧ) головкой ВА1 включается дроссель L1, индуктивное сопротивление которого прямо пропорционально частоте. Как известно, в цепях с индуктивным сопротивлением ток отстает от приложенного напряжения, а в цепях, содержащих емкость,— опережает напряжение. Следовательно, амплитуда тока и угол сдвига между током и приложенным напряжением не остаются постоянными и находятся в сложной зависимости от частоты.
Например, для простых разделительных фильтров фазочастотная характеристика (ФЧХ) имеет вид, представленный на рис. 1, в. В зоне совместного действия 50…5000 Гц, в зависимости от частоты, угол (р сдвига фаз между токами, проходящими по головкам ВА1 и ВА2, изменяется соответственно от 142 до 35°. Аналогичная картина наблюдается и между фазочастотными характеристиками головок ВА2 и ВАЗ. Угол сдвига фаз между токами головок на краях зоны совместного действия составляет 60 и 100°. Очевидно, что угол сдвига фаз между токами головок ВА1 — ВА2, ВА2 — ВАЗ чрезмерно велик и зависит от частоты, следовательно, синфазная по звуковому давлению работа головок в зоне совместного действия не обеспечена. .
Если ток в первой головке изменяется по закону Ii sin ot, а во второй—l2 sin (o)t+cpi2), следовательно, между токами динамических головок существует фазовый сдвиг на угол (pi2 и в этом случае в окружающем пространстве звуковое давление будет пропорционально так называемому эквивалентному току Iэ
IЭ = I1 sin ωt + I2 sin(ωt + φ1-2) = IM sin (ωt + α),
амплитуда которого IM определяется из выражения:
IM = корень.кв(I12 + I22 + I1I2 cos φ1-2),
а угол между эквивалентным током и током первой головки можно определить таким образом:
tg α = (I2 sin φ1-2) / (I1 + I2 cos φ1-2),
т. е. угол а зависит не только от угла сдвига фаз между составными токами (pi2, но и от соотношения их амплитуд I1 / I2. В зоне совместного действия динамических головок угол сдвига фаз может изменяться в пределах от 0 до φ1-2 в зависимости от соотношения амплитуд токов и, следовательно, при звуковоспроизведении будут внесены искажения оригинала записи.
Рис. 2. Разделительный фильтр второго порядка: а — принципиальная схема; б — амплитудно-частотная характеристика низкочастотной динамической головки ВА1
1 — основной вариант по схеме рис. 2.a. (L1 = 7,9 мГн, R1 = 1,45 Ом, СЗ = 50 мкФ, Рд= 5,5 Ом R2=0)
2—то же, но при СЗ = 100 мкФ
3—то же, но при С3 = 25 мкФ
4—то же, но при R2 = 5 Ом
5—то же, но при R15 Ом
в—зависимость угла сдвига фаз между током нижних частот и напряжением, приложенным к фильтру:
1 — основной вариант (L 1 = 7,9 мГн, R = l1,45 Ом, С3 = 50 мкФ, Рд = 5,5 Ом, R2 = 0)
2 — то же, но при СЗ = 100 мкФ
3—то же, но при С3 = 25 мкФ
4—то же, но при R2 = 5 Ом
5— то же, но при R1 = 5 Ом
Применение разделительных фильтров второго порядка повышает крутизну спада амплитудночастотных характеристик и уменьшает зону совместного действия динамических головок. Тем самым создаются условия для более четкого разделения частот. Для низкочастотного разделительного фильтра второго порядка (рис. 2,а) полное сопротивление динамической головки ВА1 равно
ZД = RД + j XД = RД + j 2π f L1,
где Rд, Хд и Lд — активное, индуктивное сопротивление и индуктивность катушки динамической головки. Полное сопротивление дросселя L1:
ZL = Z1-2 = R1j XL1 = R1 + j 2π f L1,
где L1 — индуктивность дросселя; R1 — суммарное активное сопротивление обмотки дросселя и дополнительно включаемого регулировочного резистора.
Реактивное сопротивление емкости конденсатора СЗ равно
XC3 = j(1 / 2π f C3)
Ток, проходящий через динамическую головку между точками 2, 3, равен
При известных параметрах элементов разделительного фильтра и динамической головки могут быть рассчитаны и построены амплитудно и фазочастотные характеристики (рис. 2 б, в).
В формуле (1) присутствуют реактивные сопротивления конденсатора СЗ, дросселя L1 и катушки динамической головки ВА1, которые находятся в сложной зависимости от частоты. Вследствие этого в фильтрах второго порядка угол сдвига фаз между током динамической головки и приложенным напряжением не остается постоянным и в зависимости от частоты изменяется в широких пределах. Так, например, для низкочастотного разделительного фильтра угол сдвига фаз между током динамической головки и приложенным к фильтру напряжением в зависимости от частоты может изменяться в пределах от —10 до —270° на частотах 20 и 20000 Гц соответственно (рис. 2, в). Для среднечастотной динамической головки этот угол может изменяться от +110 до —75° на частотах 80 и 20000 Гц (рис. 3), а для высокочастотной—от +135 до —50° (на 150 и 20000 Гц).
Рис. 3. Разделительный фильтр средних частот второго порядка:
а — принципиальная схема; б—зависимость угла сдвига фаз между током и напряжением, приложенным к фильтру: / — основной вариант (С4 =40 мкФ. L2=0,9 мГн, R4=0,75 Ом, Кд=б.З Ом, R3=0)
2 — то же, но при С4=20 мкФ
3 — то же, но при С4=20 мкФ ( в статье видимо опечатка)
4—то же, но при C4=80 мкФ
5—то же, но при L2=0,6 мкФ
6—то же, но при R3=5 Ом
Таким образом, угол сдвига фаз между током низкочастотной динамической головки и напряжением, приложенным к фильтру, при изменении частоты подаваемого напряжения может изменяться . на 260°, а для среднечастотной и высокочастотной головок этот же угол изменяется на 185°. Это обстоятельство является основной причиной несинфазной работы динамических головок в зоне их совместного действия.
Изменением параметров элементов разделительных фильтров можно регулировать фазочастотную характеристику каждой динамической головки. Благодаря этому имеется возможность получения идентичных характеристик головок и, тем самым, обеспечения условий синфазности их работы в зоне совместного действия. Так для низкочастотного разделительного фильтра по схеме рис. 2,а фазочастотная характеристика претерпевает следующие изменения:
при увеличении емкости конденсатора СЗ (кривая 2) центральная часть характеристики смещается параллельно влево;
уменьшение емкости конденсатора СЗ (кривая 3) смещает параллельно центральную часть характеристики вправо;
при увеличении сопротивления резистора R1 и уменьшении индуктивности дросселя L1 левая часть смещается в область малых значений углов с одновременным смещением центральной части вправо (кривая 5);
включение резистора R2 последовательно с конденсатором СЗ смещает правую часть характеристики (кривая 4) в область меньших углов.
При изменении параметров разделительных фильтров происходит коррекция не только фазочастотной характеристики, но и деформация амплитудночастотной характеристики. Так, на рис. 2,6:
от увеличения емкости конденсатора СЗ (кривая 2) незначительно возрастает амплитуда тока, полоса пропускания частот уменьшается; при уменьшении емкости конденсатора СЗ (кривая 3) ток уменьшается, а полоса пропускания увеличивается;
увеличение сопротивления резистора R1 снижает максимальное значение амплитуды тока, не оказывая влияния на полосу пропускания фильтра (кривая 5);
уменьшение индуктивности дросселя L1 сопровождается увеличением амплитуды тока и расширением полосы пропускания фильтра и т. д.
Электрические схемы разделительных фильтров для среднечастотной и высокочастотной динамических головок могут быть одинаковыми, отличаясь лишь значением параметров элементов (рис. 3,а). Для такой схемы значение силы тока головки может быть рассчитано по формуле
При емкости конденсатора С4 = 40 мкФ для динамической головки ЗГД1 фазочастотная характеристика похожа по форме на характеристику низкочастотной головки, однако она смещена в область положительных значений углов. Изменение параметров элементов разделительного фильтра оказывает влияние на фазочастотную характеристику (рис. 3,6) следующим образом:
увеличение емкости конденсатора С4 (кривая 4) смещает центральную часть характеристики в область низких частот;
уменьшение индуктивности дросселя L2 (кривая 5) смещает центральную часть в область высоких частот и левый конец характеристики в область меньших значений углов φ;
увеличение активного сопротивления головки RД (или сопротивления резистора, включенного последовательно с ней) перемещает всю характеристику параллельно в сторону увеличения угла сдвига тока;
увеличение сопротивления резистора R3 (кривая 6) спрямляет характеристику, смещая правую и левую части в сторону меньших значений угла.
Влияние изменений параметров этих же элементов на амплитудно-частотную характеристику следующее:
увеличение емкости конденсатора С4 ведет к возрастанию максимального значения амплитуды характеристики, резкому повышению ее неравномерности, зона пропускания увеличивается в сторону низких частот;
увеличение активного сопротивления головки RД в незначительной степени снижает неравномерность АЧХ;
увеличение сопротивления резистора R4 снижает неравномерность АЧХ и одновременно смещает ее в сторону низких частот;
сопротивление R3 сглаживает неравномерность характеристики.
При известных закономерностях влияния изменений параметров элементов разделительных фильтров на их фазо и амплитудно-частотные характеристики, создание идентичных (совмещенных) фазовых характеристик низкочастотной и среднечастотной динамических головок не представляет особых затруднений.
Наибольшую трудность вызывает согласование фазовых характеристик высокочастотной и среднечастотной динамических головок. Оба разделительных фильтра емкостные и, естественно, идентичность их фазочастотных характеристик может наступить при одинаковых значениях емкостей конденсаторов С4, а это противоречит условию разделения частот. Поэтому одним из вариантов является установка в высокочастотном фильтре конденсатора С4 малой емкости (около 2 мкФ) и дросселя L2 с незначительной индуктивностью (менее 0,1 мГн). Изменение емкости конденсатора С4 оказывает резкое влияние на фазовую и амплитудную характеристики. Кроме этого, могут проявляться резонансные явления, поэтому необходимо принимать меры к уменьшению неравномерности АЧХ, например, включить последовательно с конденсатором С4 (на рис. 3) резистор R3 с небольшим сопротивлением.
Вторым вариантом фазового согласования токов головок ВА2 и ВАЗ является построение фильтров по разным схемам: Например, головку ВАЗ можно включить через разделительный фильтр третьего порядка
Рис. 4. Схемы измерения полного сопротивления катушек динамических головок:
а — измерение методом замещения; б — измерение с источником напряжения
Порядок расчета фазо и амплитудно-частотных характеристик акустических систем может быть следующим. Во первых, для выполнения расчета необходимо знать активные и индуктивные сопротивления каждой динамической головки на частотах в зоне их полезной работы. Активное сопротивление может быть измерено мостом постоянного тока, омметром или другим прибором. Определение индуктивного сопротивления динамических головок связано с некоторыми трудностями, так как оно находится в сложной зависимости от частоты и от условий монтажа головки. Поэтому индуктивное сопротивление динамических головок следует определять при нормальных условиях их работы (смонтированных в ящике с закрытой задней стенкой и т. д.). На практике индуктивное сопротивление динамических головок определяется экспериментально-расчетным путем. Для этого производят измерение полного сопротивления головки по схеме рис. 4. Активное вспомогательное сопротивление г в схеме рис. 4,а должно быть больше, а в схеме рис. 4,6 — меньше ожидаемого сопротивления головки в 10…20 раз. По указанным схемам снимается зависимость полного сопротивления динамической головки от частоты.
По схеме рис. 4,а измерение осуществляется методом замещения. Устанавливая через определенные интервалы частоту звукового генератора G, вольтметром PV замеряется падение переменного напряжения на сопротивление катушки динамической головки ВА. Затем вместо головки включается переменный резистор R и, изменением его сопротивления добиваются получения на нем того же значения напряжения. В этом случае активное сопротивление R равно полному сопротивлению 2д1 динамической головки на данной частоте. Количество точек измерения определяется типом головки (НЧ, ВЧ) и неравномерностью ее характеристики.Пополученному значению полного сопротивления для каждого значения частоты индуктивное сопротивление динамической головки определяется по формуле
Xдi = кор.кв(Zдi2 — Rд2)
Уровень выходного напряжения звукового генератора влияния на результаты измерений почти не оказывает. Так, при изменении напряжения от 1 до 30 В полное сопротивление динамической головки изменяется на 5… 8 %. Измерения по схеме рис. 4,6 более точные, величина полного сопротивления головки равна
Zдi = r Uдi / Ur
По определенным значениям сопротивлений динамических головок для конкретных, частот и предполагаемым параметрам элементов разделительных фильтров по формулам (1) и (2) рассчитываются фазочастотные и амплитудночастотные характеристики. По построенным амплитудным характеристикам определяются граничные частоты раздела и зоны совместного действия динамических головок, а также неравномерность характеристик и необходимость в их выравнивании. По этим же характеристикам можно сделать заключение о крутизне разделения частот, об оценке качеств разделительных фильтров и о путях желательного изменения (смещения, сужения и т. д.).
Затем строятся фазовые характеристики и обращается особое внимание на их сближение в зоне совместного действия динамических головок. После анализа по
строенных характеристик и при наличии каких либо недостатков, на основе известного характера воздействия изменения элементов разделительных фильтров на их характеристики, намечается вариант корректировки и вновь просчитываются характеристики. Полученные характеристики строятся, анализируются и т. д. до получения необходимых результатов. Затем все элементы акустической системы монтируются и проводятся электрические испытания.
По изложенной методике нами были определены параметры разделительных фильтров для акустической системы на динамических головках: 6ГД2 (L1 = 7,9 мГн, R2 = 1Ом, С3 = 30 мкФ, Rд = 5,5 Ом, R1 = 1,45 Ом); ЗГД1 (L2 = 1,3 мГн, R4 = 1 Ом, С4 = 60 мкФ, Rд6,8 Ом, R3 = 2 Oм); 1ГДЗ (L2 = 0,08 мГн, R4 = 0,5 Ом, С4 = 2мкФ, Rд = 8,70м, R3 = 1 Ом).
На рис. 5 и 6 представлены измеренные характеристики низкочастотной (НЧ — 6ГД2) и среднечастотной (СЧ—ЗГД1) динамических головок. Как видим, граничная частота деления fP1 = 400 Гц, зона совместного действия 80…2000 Гц, а угол сдвига — между фазочастотными характеристиками составляет 150…190°. Следовательно, необходимо поменять полярность включения одной из динамических головок (“повернуть” ток на 180°). Как станет ясным из согласования среднечастотной головки с высокочастотной, следует изменить полярность включения среднечастотной головки (рис. 6, перевернутая СЧхарактеристика). В этом случае угол сдвига фаз между токами головок составляет 30 и 10° соответственно на частотах 80 и 2000 Гц. Для более точного совмещения характеристик в зоне 500…2000 Гц следует увеличить сопротивление R2 до 1,3 Ом (см. рис. 2,а). Аналогично выполнено согласование фазовых характеристик средне и высокочастотной динамических головок.
В результате согласования фазовых характеристик низко, средне и высокочастотной динамических головок представляется возможным создание акустической системы с высококачественным воспроизведением всего диапазона частот и “кажущимся” расширением диапазона воспроизводимых частот.
При изготовлении разделительных фильтров в качестве конденсаторов СЗ и С4 необходимо использовать бумажные конденсаторы на рабочее напряжение не менее 100 В, например МБГП2 на 160 В. Резисторы R1—R4 можно выполнить проводом диаметром 0,4…0,6 мм из любого высокоомного сплава; намотка производится бифилярно.
Дроссель в ВЧ фильтре выполняется на любом цилиндрическом каркасе медным проводом диаметром 0,6. ..0,8мм (около 140 витков). Дроссель L2 СЧ фильтра (примерно 240 витков) выполняется проводом диаметром 0,8 мм, активное сопротивление которого не должно превышать сопротивления резистора R4, так как на схеме под R4 обозначено активное суммарное сопротивление обмотки дросселя и дополнительного резистора. Если величина индуктивности окажется недостаточной при требуемом значении активного сопротивления, в катушку вставляется небольшой ферритовый сердечник.
Дроссель L1 низкочастотного фильтра выполняется на каркасе средних размеров (наружный диаметр 25… 30 мм) проводом 0,8 мм. Активное сопротивление обмотки 1,45 Ом. Для повышения индуктивности в катушку вставляется ферритовый П-образный сердечник от трансформатора строчной развертки. Сердечники из других материалов (трансформаторная сталь, карбонильное железо и т. п.) применять не следует, так как с ними проявляется зависимость значения индуктивности от силы или от частоты тока. Это может привести к появлению нелинейных искажений.
Соединительные провода в фильтрах должны иметь сечение не менее 0,8 мм2, а для соединения с усилительной аппаратурой—не менее 1,5 мм2. Это необходимо для снижения потерь напряжения и мощности в проводах и устранения возможных взаимных влияний между фильтрами.
Совершенно недопустимо использование отдельных элементов в схемах двух фильтров, например, конденсатор С4 высокочастотного фильтра включать после аналогичного конденсатора среднечастотного фильтра (как это часто практически делается). Если это условие не выполнять, появляются взаимные влияния на амплитудные и особенно на фазочастотные характеристики.
Ферритовый фильтр
Ферритовые кольца – это пассивный способ борьбы с синфазными помехами. Когда стоит задуматься о пассивных способах борьбы с помехами? Тогда, когда требуется наличие:
- любой конструкции, в которой длина проводов как силовых, так и сигнальных большая (от 30–40 см) и при этом нет экранов в виде алюминиевых или карбоновых лучей, экранированного кабеля;
- длинных слаботочных цепей;
- мощной передающей аппаратуры (600–800 МВт и более).
Ферритовые кольца фильтра синфазных помех обладают овальной формой для простоты монтажа. Через отверстие в кольце продеваются все три фазные жилы моторного кабеля.
Что такое фильтр?
Фильтр – это схема, которая удаляет или «отфильтровывает» определенный диапазон частотных компонентов. Другими словами, он разделяет спектр сигнала на частотные составляющие, которые будут передаваться дальше, и частотные составляющие, которые будут блокироваться.
Если у вас нет большого опыта анализа частотной области, вы можете быть не уверены в том, что представляют собой эти частотные компоненты и как они сосуществуют в сигнале, который не может иметь несколько значений напряжения одновременно. Давайте рассмотрим краткий пример, который поможет прояснить эту концепцию.
Давайте представим, что у нас есть аудиосигнал, который состоит из идеальной синусоидальной волны 5 кГц. Мы знаем, как выглядит синусоида во временной области, а в частотной области мы не увидим ничего, кроме частотного «всплеска» на 5 кГц. Теперь предположим, что мы включили генератор на 500 кГц, который вносит в аудиосигнал высокочастотный шум.
Сигнал, видимый на осциллографе, будет по-прежнему представлять собой только одну последовательность напряжений с одним значением на момент времени, но он будет выглядеть по-другому, поскольку его изменения во временной области теперь должны отражать как синусоидальную волну 5 кГц, так и высокочастотные колебания шума.
Однако в частотной области синусоида и шум являются отдельными частотными компонентами, которые присутствуют одновременно в этом одном сигнале. Синусоидальная волна и шум занимают разные участки представления сигнала в частотной области (как показано на диаграмме ниже), и это означает, что мы можем отфильтровать шум, направив сигнал через схему, которая пропускает низкие частоты и блокирует высокие частоты.
Рисунок 3 – Представление аудиосигнала и высокочастотного шума в частотной области
Русские Блоги
[Руководство]: предыдущая статья о дизайне IIR, у меня все еще есть друг, щелкнув по ней, чтобы прочитать. Хотя я не знаю, что думают судьи, но, думая, что всегда будет оценка, я решил продолжить эту серию. В этой статье поговорим об усредняющем фильтре, который на первый взгляд очень прост. Однако я лично считаю, что некоторые ключевые моменты могут быть не полностью поняты.В этой статье основное внимание уделяется внутреннему механизму и сценариям применения конструкции одномерного среднего фильтра xx.
Примечание. Постарайтесь писать аннотации к каждой статье для удобства чтения. В век информации время каждого ценится, и это также может сэкономить драгоценное время поклонников.
Чтобы узнать что-то одно, личный совет должен быть основан на трех аспектах:What Why How
Содержание здесь в основном относится к разделу 7.5.1 «Введение в цифровую обработку сигналов», составленному Ху Гуаншу с некоторым собственным пониманием.
Когда дело доходит до фильтров усреднения, друзья, которые занимались разработкой приложений для микроконтроллеров, могут сразу подумать о добавлении и усреднении некоторых выборочных данных. Действительно, это также очень интуитивно понятно из математического описания временной области: KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ y(n)&=\frac{1}… где x ( n ) x(n) x(n)Представляет текущее измеренное значение. Для однокристальных приложений это может быть текущее значение выборки АЦП или ряд физических величин, обрабатываемых датчиком тока (например, температура, давление, расход и другие измеренные значения в области промышленного управления. ). x ( n − 1 ) x(n-1) x(n−1)Указывает последнее измеренное значение и т. Д. x ( n − N + 1 ) x(n-N+1) x(n−N+1)Это предыдущее значение N-1 измерения.
Чтобы раскрыть более глубокий механизм, передаточная функция Z используется для дальнейшего описания приведенной выше формулы: KaTeX parse error: No such environment: align* at position 8: \begin{̲a̲l̲i̲g̲n̲*̲}̲ H(Z)&=\frac{1}… Для преобразования Фурье: X ( ω ) = ∑ k = − ∞ ∞ x ( n ) e − j ω n X(\omega)=\sum_{k=-\infty}^{\infty}x(n)e^{-j\omega{n}} X(ω)=k=−∞∑∞x(n)e−jωn Суть Z-преобразования — это дискретная форма преобразования Лапласа, Z = e σ + j ω = e σ e j ω Z=e^{\sigma+j\omega}=e^{\sigma}e^{j\omega} Z=eσ+jω=eσejω,делать e σ = r e^{\sigma}=r eσ=r,тогда X ( Z ) = ∑ k = − ∞ ∞ x ( n ) ( r e j ω ) − n X(Z)=\sum_{k=-\infty}^{\infty}x(n)(re^{j\omega})^{-n} X(Z)=k=−∞∑∞x(n)(rejω)−n Заказать r = 1 r=1 r=1,тогда X ( Z ) = ∑ k = − ∞ ∞ x ( n ) e j ω n X(Z)=\sum_{k=-\infty}^{\infty}x(n)e^{j\omega{n}} X(Z)=k=−∞∑∞x(n)ejωn Следовательно, частотная характеристика среднего фильтра:
Используйте следующий код Python для анализа
# encoding: UTF-8 from scipy.optimize import newton from scipy.signal import freqz, dimpulse, dstep from math import sin, cos, sqrt, pi import numpy as np import matplotlib.pyplot as plt import sys reload(sys) sys.setdefaultencoding(‘utf8’) # Функция используется для расчета частоты среза фильтра скользящего среднего def get_filter_cutoff(N, **kwargs): func = lambda w: sin(N*w/2) — N/sqrt(2) * sin(w/2) deriv = lambda w: cos(N*w/2) * N/2 — N/sqrt(2) * cos(w/2) / 2 omega_0 = pi/N # Starting condition: halfway the first period of sin return newton(func, omega_0, deriv, **kwargs) # Установить частоту дискретизации sample_rate = 200 #Hz N = 7 # Рассчитать частоту среза w_c = get_filter_cutoff(N) cutoff_freq = w_c * sample_rate / (2 * pi) # Параметры фильтра b = np.ones(N) a = np.array([N] + [0]*(N-1)) #Частотный отклик w, h = freqz(b, a, worN=4096) # Перейти к частоте w *= sample_rate / (2 * pi) # Рисование диаграммы Боде plt.subplot(2, 1, 1) plt.suptitle(«Bode») # Преобразовать в децибелы plt.plot(w, 20 * np.log10(abs(h))) plt.ylabel(‘Magnitude [dB]’) plt.xlim(0, sample_rate / 2) plt.ylim(-60, 10) plt.axvline(cutoff_freq, color=’red’) plt.axhline(-3.01, linewidth=0.8, color=’black’, linestyle=’:’) # Фазовая частотная характеристика plt.subplot(2, 1, 2) plt.plot(w, 180 * np.angle(h) / pi) plt.xlabel(‘Frequency [Hz]’) plt.ylabel(‘Phase [°]’) plt.xlim(0, sample_rate / 2) plt.ylim(-180, 90) plt.yticks([-180, -135, -90, -45, 0, 45, 90]) plt.axvline(cutoff_freq, color=’red’) plt.show()
Частота дискретизации составляет 200 Гц, а длина фильтра — 7, чтобы получить следующие кривые амплитудно-частотной и фазо-частотной характеристики. По его главному лепестку видно, что его амплитудно-частотная характеристика представляет собой фильтр нижних частот. Амплитудно-частотная характеристика немного неравномерна и ослабевает с увеличением частоты. Его фазовая частотная характеристика линейна. Друзья, имеющие опыт работы с фильтрами, знают, что частотно-фазовая характеристика КИХ-фильтров линейна, а фильтр скользящего среднего — это просто частный случай КИХ-фильтров.
При изменении длины фильтра на 3/7/21 наблюдайте только его амплитудно-частотную характеристику:
Можно видеть, что по мере увеличения длины фильтра его частота среза становится меньше, а полоса пропускания сужается. Реакция фильтра становится медленнее, а задержка увеличивается. Следовательно, при фактическом использовании длина фильтра должна быть разумно выбрана в соответствии с полезной полосой частот. Полоса пропускания полезного сигнала может быть получена с помощью анализа Фурье путем сбора определенной точки в соответствии с частотой дискретизации. Если у вас есть осциллограф с функцией БПФ, вы также можете напрямую измерить его.
Реализация фильтра на языке C относительно проста. Здесь снова используется общий код:
#define MVF_LENGTH 5 typedef float E_SAMPLE; / * Определяем историческое состояние регистра скользящей средней * / typedef struct _t_MAF { E_SAMPLE buffer[MVF_LENGTH]; E_SAMPLE sum; int index; }t_MAF; void moving_average_filter_init(t_MAF * pMaf) { pMaf->index = -1; pMaf->sum = 0; } E_SAMPLE moving_average_filter(t_MAF * pMaf,E_SAMPLE xn) { E_SAMPLE yn=0; int i=0; if(pMaf->index == -1) { for(i = 0; i < MVF_LENGTH; i++) { pMaf->buffer
= xn; } pMaf->sum = xn*MVF_LENGTH; pMaf->index = 0; } else { if(xn>100) xn = xn+0.1; pMaf->sum -= pMaf->buffer[pMaf->index]; pMaf->buffer[pMaf->index] = xn; pMaf->sum += xn; pMaf->index++; if(pMaf->index>=MVF_LENGTH) pMaf->index = 0; } yn = pMaf->sum/MVF_LENGTH; return yn; }
Код теста:
#define SAMPLE_RATE 500.0f #define SAMPLE_SIZE 256 #define PI 3.415926f int main() { E_SAMPLE rawSin[SAMPLE_SIZE]; E_SAMPLE outSin[SAMPLE_SIZE]; E_SAMPLE rawSquare[SAMPLE_SIZE]; E_SAMPLE outSquare[SAMPLE_SIZE]; t_MAF mvf; FILE *pFile=fopen(«./simulationSin.csv»,»wt+»); / * Тест прямоугольной волны * / if(pFile==NULL) { printf(«simulationSin.csv opened failed»); return -1; } for(int i=0;i<SAMPLE_SIZE;i++) { rawSin
= 100*sin(2*PI*20*i/SAMPLE_RATE)+rand()%30; } / * Тест синусоидального сигнала * / for(int i=0;i<SAMPLE_SIZE/4;i++) { rawSquare = 5+rand()%10; } for(int i=SAMPLE_SIZE/4;i<3*SAMPLE_SIZE/4;i++) { rawSquare = 100+rand()%10; } for(int i=3*SAMPLE_SIZE/4;i<SAMPLE_SIZE;i++) { rawSquare = 5+rand()%10; } / * инициализация * / moving_average_filter_init(&mvf); / * Фильтрация * / for(int i=0;i<SAMPLE_SIZE;i++) { outSin=moving_average_filter(&mvf,rawSin); } for(int i=0;i<SAMPLE_SIZE;i++) { fprintf(pFile,»%f,»,rawSin); } fprintf(pFile,»\n»); for(int i=0;i<SAMPLE_SIZE;i++) { fprintf(pFile,»%f,»,outSin); } fclose(pFile); pFile=fopen(«./simulationSquare.csv»,»wt+»); if(pFile==NULL) { printf(«simulationSquare.csv opened failed»); return -1; } / * инициализация * / moving_average_filter_init(&mvf); / * Фильтрация * / for(int i=0;i<SAMPLE_SIZE;i++) { outSquare=moving_average_filter(&mvf,rawSquare); } for(int i=0;i<SAMPLE_SIZE;i++) { fprintf(pFile,»%f,»,rawSquare); } fprintf(pFile,»\n»); for(int i=0;i<SAMPLE_SIZE;i++) { fprintf(pFile,»%f,»,outSquare); } fclose(pFile); return 0; }
Для теста прямоугольной волны используйте Excel, чтобы сгенерировать форму волны, и можно получить следующую форму волны. Из формы волны очевидно, что фильтр скользящего среднего с длиной 7 относительно удовлетворителен для эффекта фильтрации случайного шума. Из рисунка также видно, что фильтр скользящего среднего вносит определенную задержку в цепочку сигналов, которую необходимо учитывать при его применении. Если нет четких требований к общему измерению датчика, его часто можно игнорировать.
Для синусоидальных сигналов фильтр скользящего среднего также имеет более очевидный эффект, но его полоса пропускания относительно узкая. Если частота полезного сигнала относительно высока, фильтр скользящего среднего не подходит.
подводить итоги:
- Фильтр скользящего среднего хорошо работает при фильтрации высокочастотного шума.
- Фильтр скользящего среднего — это, по сути, КИХ-фильтр с линейной фазовой частотной характеристикой.
- При практическом использовании следует обращать внимание на частоту полезного сигнала, если частота полезного сигнала выше, это неприменимо.
- Длина не должна быть слишком большой, иначе эффект задержки будет большим.
- С точки зрения сигнальной цепи его можно использовать в качестве предварительной обработки, то есть данные после прямой фильтрации АЦП. Его также можно использовать в качестве пост-обработки.
- Если это фильтрация данных выборки АЦП, выборка целочисленная, код в тексте можно оптимизировать соответствующим образом, например, умножение и деление можно заменить сдвигом влево и сдвигом вправо.
Заявление об авторских правах: Авторские права на все статьи принадлежат встроенному отелю, например, коммерческое использование должно быть разрешено встроенным отелем. Приглашаем подписаться на официальный аккаунт WeChat, контент богаче.
Порядок фильтра и его добротность
Следующий параметр, с которым надо определиться — это порядок фильтра и его добротность. В данной статье будут рассматриваться два порядка, первый и второй.
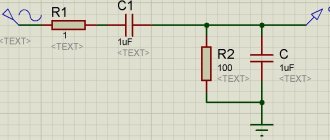
- С первым все просто: есть катушка, есть конденсатор, считаем их параметры под требуемую частоту среза и при надобности корректируем значения до получения желаемой АЧХ, ФЧХ, ИЧХ.
- Со вторым порядком по-хитрее, там уже две катушки и два конденсатора. От значений номиналов зависит такой параметр как добротность, он определяет крутизну спада АЧХ и в некоторой степени сдвиг фазы. Поскольку влияние фазового сдвига и крутизны умозрительно не прикинешь, остается просто выбрать в какую сторону думать. А думать тут в сторону низкой добротности, читай больше индуктивности в катушках, меньше емкости в конденсаторах.
Как выбрать порядок. Тут руководствуются уже знакомыми соображениями о том, на что способны излучатели, в особенности высокочастотник. Если большой ход ему противопоказан (как в нашем случае) то предпочтение отдаем второму порядку.
Для полноты картины следует упомянуть, что порядок также определяет степень совместной работы динамиков, но это уже информация для самостоятельного размышления.
Фильтры. Фаза и её производная
Вот теперь, когда у нас накопилось некоторое количество материала, можно заняться фазой. Надо с самого начала сказать, что давным-давно понятие фазы ввели для обслуживания нужд электротехники.
Когда сигнал представляет собой чистый синус (хотя степень чистоты бывает разная) фиксированной частоты, то вполне естественно представить его в виде вращающегося вектора, определяемого, как известно, амплитудой (модулем) и фазой (аргументом). Для звукового сигнала, в котором синусы присутствуют лишь в виде разложения, понятие фазы уже не столь наглядно. Однако не менее полезно — хотя бы потому, что звуковые волны от разных источников складываются векторно. А теперь посмотрим, как выглядят фазочастотные характеристики (ФЧХ) фильтров до четвёртого порядка включительно. Нумерация рисунков будет сохраняться сквозная, с прошлого выпуска.
Начинаем, стало быть, с рис. 12 и 13.
рис. 12
рис. 13
Сразу можно подметить любопытные закономерности.
1. Любой фильтр «крутит» фазу на угол, кратный π/4, точнее говоря, на величину (nπ)/4, где n — порядок фильтра.
2. ФЧХ фильтра НЧ всегда начинается от 0 градусов.
3. ФЧХ фильтра ВЧ всегда приходит на 360 градусов.
Последний пункт можно уточнить: «точка назначения» ФЧХ фильтра верхних частот кратна 360 градусам; если порядок фильтра выше четвёртого, то с ростом частоты фаза фильтра ВЧ будет стремиться к 720 градусам, то есть к 4π, если выше восьмого — к 6π и т. д. Но для нас это уже чистая математика, имеющая к практике весьма отдалённое отношение.
Из совместного рассмотрения перечисленных трёх пунктов нетрудно заключить, что ФЧХ фильтров ВЧ и НЧ совпадают лишь для чётвёртого, восьмого и т.д. порядков, а справедливость этого утверждения для фильтров четвёртого порядка наглядно подтверждает и график на рис. 13. Впрочем, из этого факта не следует, что фильтр четвёртого порядка «самый лучший», как, кстати, не следует и обратного. И вообще, выводы пока делать рано.
Фазовые характеристики фильтров не зависят от способа реализации — активные они или пассивные, и даже от физической природы фильтра. Поэтому мы не будем специально заострять внимание на ФЧХ пассивных фильтров, они по большей части ничем не отличаются от тех, что мы уже видели. Кстати говоря, фильтры относятся к числу так называемых минимально-фазовых цепей — их амплитудно-частотные и фазочастотные характеристики жёстко взаимосвязаны. К числу неминимально-фазовых звеньев относится, к примеру, линия задержки.
Совершенно очевидно (при наличии графиков), что чем выше порядок фильтра, тем его ФЧХ падает круче. А крутизну любой функции характеризуют чем? Её производной. Производная ФЧХ по частоте имеет специальное название — групповое время задержки (ГВЗ). Фазу надо брать в радианах, а частоту — не колебательную (в герцах), а угловую, в радианах в секунду. Тогда производная получит размерность времени, что объясняет (правда, частично) её название. Характеристики ГВЗ у однотипных фильтров ВЧ и НЧ ничем не отличаются. Вот так выглядят графики ГВЗ для фильтров Баттерворта с первого порядка по четвёртый (рис. 14).
рис. 14
Тут разница между фильтрами разных порядков кажется особенно заметной. Максимальное (по амплитуде) значение ГВЗ для фильтра четвёртого порядка примерно вчетверо больше, чем у фильтра первого порядка и вдвое больше — чем у фильтра второго. Встречаются высказывания, что по этому параметру фильтр четвёртого порядка как раз вчетверо хуже, чем фильтр первого. Для фильтра ВЧ — возможно. Но для фильтра НЧ минусы высокого ГВЗ не столь существенны в сравнении с плюсами высокой крутизны спада АЧХ.
Для дальнейшего изложения нам полезно будет представлять себе, как выглядит ФЧХ «по воздуху» электродинамической головки, то есть как зависит фаза излучения от частоты.
рис. 15
Примечательная картинка (рис. 15): на первый взгляд как у фильтра, но, с другой стороны, это вовсе и не фильтр — фаза всё время падает, причём с растущей крутизной. Не буду напускать лишнюю таинственность: так выглядит ФЧХ линии задержки. Люди опытные скажут: понятное дело, задержка обусловлена пробегом звуковой волны от излучателя до микрофона. И ошибутся опытные люди: микрофон у меня был установлен по фланцу головки; если даже брать в расчёт положение так называемого центра излучения, то это может вызвать погрешность 3 — 4 см (для данной конкретной головки). А тут, если прикинуть, задержка почти на полметра. А, собственно, почему её (задержки) не должно быть? Вот представьте себе на выходе усилителя такой сигнал: ничего-ничего, и вдруг синус — как ему и положено, из начала координат и с максимальной крутизной. (Мне, например, и представлять ничего не надо, у меня на одном из измерительных CD такое записано, мы по этому сигналу полярность проверяем.) Понятно, ток через звуковую катушку потечёт не сразу, у неё ещё какая-то индуктивность есть. Но это мелочи. Главное, что звуковое давление — это объёмная скорость, то есть диффузору надо сперва разогнаться, и только потом появится звук. Для величины задержки, наверное, можно вывести формулу, наверняка там будут фигурировать масса «подвижки», силовой фактор и, возможно, омическое сопротивление катушки. Кстати, подобные результаты я получал на разном оборудовании: как на аналоговом фазометре Bruel & Kjaer, так и на цифровых комплексах MLSSA и Clio. Точно знаю, что у среднечастотников задержка меньше, чем у басовиков, а у пищалок меньше, чем у тех и этих. Как ни удивительно, но в литературе я ссылок на подобные результаты не встречал.
Зачем я привёл этот поучительный график? А затем, что если дело действительно обстоит именно так, как мне видится, то многие рассуждения о свойствах фильтров теряют практический смысл. Хотя я их всё же изложу, а вы уже сами решите, все ли из них стоит принимать на вооружение.
Схемы пассивных фильтров
Думаю, мало кто удивится, если я заявлю, что схемных реализаций пассивных фильтров существует куда меньше, чем фильтров активных. Я бы сказал, что их примерно две с половиной. То есть если эллиптические фильтры выводить в отдельный класс схем, получится три, если этого не делать — то две. Причём в 90% случаев в акустике используются так называемые параллельные фильтры. Поэтому мы начнём не с них.
Последовательные фильтры, в отличие от параллельных, не существуют «по частям» — тут фильтр НЧ, а там фильтр ВЧ. А значит, вы не сможете подключить их к разным усилителям. К тому же по своим характеристикам это фильтры первого порядка. А между прочим, ещё вездесущий господин Смолл обосновал, что фильтры первого порядка для акустических применений непригодны, что бы там ни говорили ортодоксальные аудиофилы (с одной стороны) и сторонники всемерного удешевления акустической продукции (с другой). Однако у последовательных фильтров есть один плюс: сумма выходных напряжений у них всегда равна единице. Вот как выглядит схема двухполосного последовательного фильтра (рис. 16).
рис. 16
В данном случае номиналы соответствуют частоте среза 2000 Гц. Нетрудно понять, что сумма напряжений на нагрузках всегда в точности равна входному напряжению. Эта особенность последовательного фильтра используется при «подготовке» сигналов для их дальнейшей обработки процессором (в частности, в Dolby Pro Logic). На следующем графике вы видите АЧХ фильтра (рис. 17).
рис. 17
Можете поверить, что графики ФЧХ и ГВЗ у него точно такие же, как и у любого фильтра первого порядка. Науке известен и трёхполосный последовательный фильтр. Схема его на рис. 18.
рис. 18
Приведенные на схеме номиналы соответствуют той же частоте раздела (2000 Гц) между твитером (ВЧ) и среднечастотником и частоте 100 Гц — раздела между СЧ и НЧ-головками. Понятно, что трёхполосный последовательный фильтр обладает тем же свойством: сумма напряжений на его выходе в точности равна напряжению на входе. На следующем рисунке (рис. 19), где приведен набор характеристик этого фильтра, вы можете увидеть, что крутизна спада фильтра пищалки в диапазоне 50 — 200 Гц выше, чем 6 дБ/окт., поскольку его полоса тут накладывается не только на полосу СЧ, но и на полосу НЧ головки. Вот уж чего не умеют делать параллельные фильтры — у них перехлёст полос неизбежно преподносит сюрпризы, и всегда — нерадостные.
рис. 19
Параметры последовательного фильтра рассчитываются в точности так же, как и номиналы фильтров первого порядка. Зависимость всё та же (см. формулу 1.1). Удобнее всего ввести так называемую постоянную времени, через частоту среза фильтра она выражается как TO = 1/(2πFc).
Тогда
C = TO/RL (2.1), а
L = TO • RL (2.2).
(Здесь RL — импеданс нагрузки, в данном случае 4 Ом).
Если, как во втором случае, у вас трёхполосный фильтр, то частот раздела будет две и постоянных времени тоже две.
Наверное, самые технически подкованные из вас уже заметили, что я слегка «передёрнул» карты и заменил реальный импеданс нагрузки (то есть динамика) омическим «эквивалентом» 4 Ом. В действительности, конечно, никакой он не эквивалент. На самом деле даже принудительно заторможенная звуковая катушка с точки зрения измерителя импеданса выглядит как последовательно соединённые активное и индуктивное сопротивление. А когда катушка обладает подвижностью, индуктивность возрастает на высокой частоте, а вблизи частоты резонанса головки у неё как бы возрастает омическое сопротивление, случается, и в десять раз, и больше. Программ, которые умеют учитывать такие особенности реальной головки, очень немного, мне лично известно три. Но мы никоим образом не ставили своей целью научиться работать, скажем, в программной среде Linearx. У нас задача иная — разобраться с основными особенностями фильтров. Поэтому будем по старинке имитировать присутствие головки резистивным эквивалентом, и конкретно — номиналом 4 Ом. Если в вашем случае нагрузка имеет другой импеданс, то и все входящие в схему пассивного фильтра импедансы должны быть пропорционально изменены. То есть индуктивности — пропорционально, а ёмкости — обратно пропорционально сопротивлению нагрузки.
(Прочтя это в черновике, главный редактор сказал: «Ты что, последовательные фильтры — это Клондайк, давай копнём как-нибудь». Согласен. Клондайк. Пришлось обещать, что в одном из грядущих номеров отдельно и специально копнём.)
Получившие наиболее широкое распространение параллельные фильтры называют ещё «лестничными». Думаю, всем будет ясно, откуда взялось это название после того, как вы взглянете на обобщённую схему фильтра (рис. 20).
рис. 20
Чтобы получить фильтр НЧ четвёртого порядка, надо все горизонтальные «планки» в этой схеме заменить индуктивностями, а все вертикальные — емкостями. Соответственно, для построения фильтра ВЧ нужно сделать всё наоборот. Фильтры более низких порядков получаются путём отбрасывания одного или более элементов, начиная с последнего. Фильтры более высокого порядка получают аналогичным способом, только наращиванием числа элементов. Но мы с вами договоримся: выше четвёртого порядка фильтров для нас не существует. Как мы увидим позже, одновременно с ростом крутизны фильтра углубляются и их недостатки, поэтому такая договорённость не является чем-то крамольным. Для полноты изложения надо бы сказать ещё вот что. Существует альтернативный вариант построения пассивных фильтров, где первым элементом всегда ставится резистор, а не реактивный элемент. Такие схемы применяют, когда требуется нормировать входной импеданс фильтра (например, операционные усилители «не любят» нагрузку менее 50 Ом). Но в нашем случае лишний резистор — это неоправданные потери мощности, поэтому «наши» фильтры начинаются реактивностью. Если, конечно, не требуется специально снизить уровень сигнала.
Самый сложный по устройству полосовой фильтр получается, если в обобщённой схеме каждый горизонтальный элемент заменить последовательным соединением ёмкости и индуктивности (в любой последовательности), а каждый вертикальный элемент должен быть заменён параллельно включёнными — также ёмкостью и индуктивностью. Наверное, я всё-таки приведу такую вот «страшную» схему (рис. 21).
рис. 21
Есть ещё одна маленькая хитрость. Если вам понадобится несимметричный «бандпасс» (полосовой фильтр), у которого, скажем, фильтр ВЧ имеет четвёртый порядок, а фильтр НЧ — второй, то лишние детали из приведённой выше схемы (то есть один конденсатор и одну катушку) надо убирать непременно с «хвоста» схемы, а не наоборот. Иначе вы получите несколько неожиданные эффекты от изменения характера нагружения предыдущих каскадов фильтра.
Мы не успели познакомиться с эллиптическими фильтрами. Ну, значит, в следующий раз с них и начнём.
Теги: ФазаФильтры
Частота среза
Диапазон частот, для которого фильтр не вызывает значительного ослабления, называется полосой пропускания, а диапазон частот, для которых фильтр вызывает существенное ослабление, называется полосой задерживания. Аналоговые фильтры, такие как RC фильтр нижних частот, переходят из полосы пропускания в полосу задерживания всегда постепенно. Это означает, что невозможно идентифицировать одну частоту, на которой фильтр прекращает пропускать сигналы и начинает их блокировать. Однако инженерам нужен способ, чтобы удобно и кратко охарактеризовать амплитудно-частотную характеристику фильтра, и именно здесь в игру вступает понятие частоты среза.
Когда вы посмотрите на график амплитудно-частотной характеристики RC фильтра, вы заметите, что термин «частота среза» не очень точен. Изображение спектра сигнала, «разрезанного» на две половины, одна из которых сохраняется, а другая отбрасывается, неприменимо, поскольку затухание увеличивается постепенно по мере того, как частоты перемещаются от значений ниже частоты среза к значениям выше частоты среза.
Частота среза RC фильтра нижних частот фактически является частотой, на которой амплитуда входного сигнала уменьшается на 3 дБ (это значение было выбрано, поскольку уменьшение амплитуды на 3 дБ соответствует снижению мощности на 50%). Таким образом, частоту среза также называют частотой -3 дБ, и на самом деле это название является более точным и более информативным. Термин полоса пропускания относится к ширине полосы пропускания фильтра, и в случае фильтра нижних частот полоса пропускания равна частоте -3 дБ (как показано на диаграмме ниже).
Рисунок 8 – Данная диаграмма показывает общие особенности амплитудно-частотной характеристики RC фильтра нижних частот. Ширина полосы пропускания равна частоте -3 дБ.
Как объяснялось выше, пропускающее низкие частоты поведение RC фильтра обусловлено взаимодействием между частотно-независимым импедансом резистора и частотно-зависимым импедансом конденсатора. Чтобы определить подробности амплитудно-частотной характеристики фильтра, нам нужно математически проанализировать взаимосвязь между сопротивлением (R) и емкостью (C); мы также можем манипулировать этими значениями, чтобы разработать фильтр, который соответствует точным спецификациям. Частота среза (fср) RC фильтра нижних частот рассчитывается следующим образом:
\
Давайте посмотрим на простой пример. Значения конденсаторов являются более сдерживающими, чем значения резисторов, поэтому мы начнем с распространенного значения емкости (например, 10 нФ), а затем воспользуемся формулой для определения необходимого значения сопротивления. Цель состоит в том, чтобы разработать фильтр, который будет сохранять аудиосигнал 5 кГц и подавлять шум 500 кГц. Мы попробуем частоту среза 100 кГц, а позже в этой статье мы более тщательно проанализируем влияние этого фильтра на обе частотные составляющие.
\
Таким образом, резистор 160 Ом в сочетании с конденсатором 10 нФ даст нам фильтр, который дает амплитудно-частотную характеристику, близкую к необходимой.
Операционные усилители (на основе простейших примеров): часть 3
Краткое введение
Продолжаю спамить писать на тему операционных усилителей. В этой статье постараюсь дать обзор одной из важнейших тем, связанной с ОУ. Итак, добро пожаловать, активные фильтры
.
Обзор темы
Возможно, Вы уже сталкивались с моделями RC-, LC- и RLC-фильтров. Они вполне подходят для большинства задач. Но для некоторых целей очень важно иметь фильтры с более плоскими характеристиками в полосе пропускания и более крутыми склонами. Вот тут нам и нужны активные фильтры. Для освежения в памяти, напомню, какие бывают фильтры: Фильтр Нижних Частот (ФНЧ) — пропускает сигнал, который ниже определенной частоты (ее еще именуют частотой среза). Википедия Фильтр Высоких Частот (ФВЧ) — пропускает сигнал выше частоты среза. Википедия Полосовой Фильтр — пропускает только определенный диапазон частот. Википедия Режекторный Фильтр — задерживает только определенный диапазон частот. Википедия Ну еще немного лирики. Посмотрите на амплитудно-частотную характеристику (АЧХ) ФВЧ. На этом графике ничего интересного пока не ищите, а просто обратите внимание на участки и их названия: Самые банальные примеры активных фильтров можно подсмотреть здесь в разделе «Интеграторы и дифференциаторы». Но в данной статье эти схемы трогать не будем, т.к. они не очень эффективны.
Выбираем фильтр
Предположим, что Вы уже определились с частотой, которую хотите фильтровать. Теперь нужно определиться с типом фильтра. Точнее нужно выбрать его характеристику. Иными словами, как фильтр будет себя «вести». Основными характеристиками являются: Фильтр Баттерворда
— обладает самой плоской характеристикой в полосе пропускания, но имеет плавный спад.
Фильтр Чебышева
— обладает самым крутым спадом, но у него самые неравномерные характеристики в полосе пропускания.
Фильтр Бесселя
— имеет хорошую фазочастотную характеристику и вполне «приличный» спад. Считается лучшим выбором, если нет специфического задания.
Еще немного информации
Предположим, и с этим заданием вы справились. И теперь можно смело приступить к расчетам. Есть несколько методов расчета. Не будем усложнять и воспользуемся самым простым. А самый простой — это «табличный» метод. Таблицы можно найти в соответствующей литературе. Чтобы Вы долго не искали, приведу из Хоровица и Хилла «Искусство Схемотехники». Для ФНЧ:
Скажем так, это все Вы могли бы найти и прочитать и в литературе. Перейдем конкретно к проектированию фильтров.
Расчет
В данном разделе попытаюсь кратко «пробежаться» по всем типам фильтров. Итак, задание # 1
. Построить фильтр низких частот второго порядка с частотой среза 150 Гц по характеристике Баттерворда. Приступим. Если мы имеем фильтр n-ного четного порядка, это означает, что в нем будет n/2 операционников. В данном задании — один. Схема ФНЧ: Для данного типа расчета берется во внимание, что
R1 = R2
,
C1 = C2
. Смотрим в табличку. Видим, что
К = 1.586
. Это нам пригодится чуть позже. Для фильтра низких частот справедливо: , где, разумеется, — это частота среза. Сделав подсчет, получаем . Теперь займемся подбором элементов. С ОУ определились — «идеальный» в количестве 1 шт. Из предыдущего равенства можно предположить, что нам не принципиально, какой элемент выбирать «первым». Начнем с резистора. Лучше всего, чтоб его значение сопротивления были в пределах от 2кОм до 500кОм. На глаз, пусть он будет 11 кОм. Соответственно, емкость конденсатора станет равной 0.1 мкФ. Для резисторов обратной связи значение
R
берем произвольно. Я обычно беру 10 кОм. Тогда, для верхнего значение К возьмем из таблицы. Следовательно, нижний будет иметь значение сопротивления
R =
10 кОм, а верхний 5.8 кОм. Соберем и промоделируем АЧХ.
Задание # 2
. Построить фильтр высоких частот четвертого порядка с частотой среза 800 Гц по характеристике Бесселя. Решаем. Раз фильтр четвертого порядка, то в схеме будет два операционника. Тут все совсем не сложно. Мы просто каскадно включаем 2 схемы ФВЧ. Сам фильтр выглядит так: Фильтр же четвертого порядка выглядит: Теперь расчет. Как видим, для фильтра четвертого порядка у нас аж 2 значения
К
. Логично, что первое предназначается для первого каскада, второе — для второго. Значения
К
равны 1.432 и 1.606 соответсвенно. Таблица была для фильтров низких частот (!). Для расчета ФВЧ надо кое-что изменить. Коэффициенты
К
остаются такими же в любом случае. Для характеристик Бесселя и Чебышева изменяется параметр — нормирующая частота. Она будет равна теперь: Для фильтров Чебышева и Бесселя как для нижних частот, так и для высоких справедлива одна и та же формула: Учтите, что для каждого отдельного каскада придется считать отдельно. Для первого каскада: Пусть
С
= 0.01 мкФ, тогда
R
= 28.5 кОм. Резисторы обратной связи: нижний, как обычно, 10 кОм; верхний — 840 Ом. Для второго каскада: Емкость конденсатора оставим неизменной. Раз
С =
0.01 мкФ, то
R
= 32 кОм. Строим АЧХ.
Для создания полосового или режекторного типа фильтров можно каскадно соединить ФНЧ и ФВЧ. Но такими типами, зачастую, не пользуются из-за плохих характеристик. Для полосовых и режекторных фильтров также можно использовать «табличный метод», но тут немного другие характеристики. Приведу сразу табличку и немного ее объясню. Чтоб сильно не растягивать — значения взяты сразу для полосового фильтра четвертого порядка. a1
и
b1
— расчетные коэффициенты.
Q
— добротность. Это новый параметр. Чем значение добротности больше — тем более «резким» будет спад.
Δf
— диапазон пропускаемых частот, причем выборка идет на уровне -3 дБ. Коэффициент
α
— еще один расчетный коэффициент. Его можно найти используя формулы, которые довольно легко найти в интернете. Ну ладно, хватит. Теперь рабочее задание.
Задание # 3
. Построить полосовой фильтр четвертого порядка по характеристике Баттерворда с центральной частотой 10 кГц, шириной пропускаемых частот 1 кГц и коэффициентом усиления в точке центральной частоты равным 1. Поехали. Фильтр четвертого порядка. Значит два ОУ. Типовую схему приведу сразу с расчтными элементами. Для первого фильтра центральная частота определяется как: Для второго фильтра: Конкретно в нашем случае, опять же из таблицы, определяем, что добротность
Q
= 10. Рассчитываем добротность для фильтра. Причем, стоит отметить, что добротность обоих будет равна. Поправка усиления для области центральной частоты: Финальная стадия — расчет компонентов. Пусть конденсатор будет равен 10 нФ. Тогда, для первого фильтра: В том же порядке, что и (1) находим
R22 = R5 =
43.5 кОм,
R12 = R4
= 15.4 кОм,
R32 = R6
= 54.2 Ом. Только учтите, что для второго фильтра используем Ну и на последок, АЧХ.
Следующая остановка — полосно-заграждающие фильтры или режекторные. Тут есть несколько вариаций. Наверное, самый простой — это фильтр Вина-Робинсона (англ. Active Wien-Robinson Filter). Типовая схема — тоже фильтр 4го порядка. Наше последнее задание. Задание # 4
. Построить режекторный фильтр с центральной частотой 90 Гц, добротностью
Q
= 2 и коэффициентом усиления в полосе пропускания равным 1. Прежде всего, произвольно выбираем емкость конденсатора. Допустим,
С =
100 нФ. Определим значение
R6 = R7 = R
: Логично, что «играясь» с этими резисторами, мы можем изменять диапазон частот нашего фильтра. Далее, нам надо определить промежуточные коэффициенты. Находим их через добротность. Выберем произвольно резистор
R2
. В данном конкретном случае, лучше всего, чтобы он равнялся 30 кОм. Теперь можем найти резисторы, которые будут регулировать коэффициент усиления в полосе пропускания. И на последок, необходимо произвольно выбрать
R5 = 2R1
. У меня в схеме эти резисторы имеют значение 40 кОм и 20 кОм соответственно. Собственно, АЧХ:
Практически конец
Кому интересно узнать немного больше, могу посоветовать почитать Хоровица и Хилла «Искусство схемотехники». Также, D. Johnson «A handbook of active filters». Википедия Также, кому не очень нужны расчеты, а нужны именно сами фильтры, могу посоветовать полезный софт P.S. Добавлю очень полезную ссылку и ее зеркало. За линк спасибо spiritus_sancti
Сведение фильтров
Теперь начинается финальный этап — сведение фильтров. Пора намотать катушки… или не намотать? Мотать всегда лень, нет провода, каркасов, конкретных значений индуктивности. В виду этих причин поискав в хламе нашлись пары катушек на 0,8 мкг и 3 мкг — на них и пришлось строить. В крайнем случаи всегда же можно домотать или отмотать лишнее.
По графику видно, что раздел попал в район 1,8 кгц, что вполне вписывается в задуманные границы. Подбором конденсаторов удалось добиться следующего импеданса. На частоте раздела имеется два бугорка, но их высота меньше полу ома — это не критично. Это не конечный его вид, в последствии был несколько увеличен резистор в цепочке Цобеля пищалки.
На приведенных выше картинках АЧХ как самого фильтра, так и АЧХ динамиков с его включением.
Импедансная характеристика динамиков
Когда с примерными параметрами все более или менее ясно, самое время переходить к практике. Снимаем импедансную характеристику динамиков. С целью оценки сопротивления на графике имеется лесенка с шагом в один Ом. Скачек на 110 герцах это переключение с 10 Ом на 20.
Разумеется с такими горбами ни один фильтр нормально, и уж тем более расчетно работать не будет, особенно фильтр НЧ. Фильтру ВЧ этот подъем работать в общем то не мешает, однако как упоминалось ранее такой подъем на конце диапазона приведет к подъему высоких частот, в случае если усилитель имеет высокое сопротивление. Это можно использовать и во благо, оставив подъем небольшим.
Для примерного представления что от чего зависит привожу набор графиков для различных емкостей и сопротивлений. Ступенька начинается с 10 Ом.
Зная минимальное сопротивление НЧ звена, нужно привести к такому же и ВЧ звено. Тут много вариантов как соединить два резистора и цепочку Цобеля, и каждый кто решился на такой отважный шаг как сведение сам способен определить вид подключения и номиналы резисторов, поэтому описывать данную процедуру здесь излишне. Конкретно в данных колонках по результатам предварительного прослушивания решено было оставить родные резисторы на 2,2 ома и цепочку Цобеля параллельно ВЧ динамику.
No tags for this post.
Минимальное влияние на ФЧХ
Амплитудно частотная характеристика (АЧХ) фильтра Бесселя (он же Томпсона) линейна во всей полосе пропускания. Но его главным достоинством, является отсутствие вносимых фазовых искажений. Т.е. для всех частот в полосе пропускания задержка одинакова.
В плане ФЧХ он идеален для применения в звуковых цепях. Но его ложкой дегтя является самый пологий спад среди всех фильтров. Более пологий спад имеет только обычная RC-цепь.
На следующем рисунке приводится сравнение крутизны срезов фильтров разного типа: 1- Бесселя, 2 — Баттерворта, 3-Чебышева (неравномерность 0.5 дБ).
Фильтр Баттерворта имеет близкие характеристики к фильтру Бесселя, но у него более крутой спад АЧХ. За это приходится расплачиваться неодинаковостью запаздывания для разных частот..
Зависимость времени запаздывания сигнала от частот для фильтров Бесселя(1) и Баттерворда(2) второго порядка, нормированных по частоте, показаны на следующем рисунке:
Обратите внимание что на графике показана циклическая частота (омега). Для перевода в герцы необходимо умножить ее на 2π. Помимо этого используется линейный а не логарифмический масштаб по оси Х.
Но все же, фильтр Баттерворда не так уж плох. Хотя я бы не рекомендовал использовать его в звуковых цепях. Или же следует выбирать более высокую частоту среза, чтобы фазовые искажения в нужном диапазоне были минимальны. Но на практике такое не всегда возможно.