В задачах обработки сигналов часто возникает необходимость фильтрации сигналов, когда сигнал разбивается на узкополосные диапазоны. В бытовом плане мы с этим сталкиваемся при воспроизведении музыки через акустические системы, в которых каждый громкоговоритель (динамик) воспроизводит свою полосу частот, которых обычно три — низкие (НЧ), средние (СЧ) и высокие (ВЧ); для воспроизведения сверхнизких частот иногда выделяют отдельную акустическую систему под названием «сабвуфер». Конкретные границы частот зависят от реализации и ориентировочно находятся на границах 100 Гц, 1 кГц и 5 кГц. Для того, чтобы не было резких скачков громкости между динамиками, используют частичное перекрытие — когда амплитуда воспроизводимой полосы частот плавно спадает на одном, одновременно нарастая на другом. Наиболее популярными фильтрами для такого разбиения являются фильтры Линквитца-Рейли 4-го порядка, представляющих из себя два последовательно соединённых фильтра Баттерворта, изображение АЧХ которых многим хорошо знакомо:
Популярность их обусловлена простотой схемотехнической реализации и гладкой АЧХ с отсутствием пульсаций. Порядок фильтра, обуславливающий скорость затухания, обычно выбирают 4-ым.
У всех аналоговых фильтров есть недостатки — нестабильность параметров и сложность в настройке. Другой немаловажным недостатком является неустранимый сдвиг фаз. Реализовать фазолинейный фильтр в аналоге невозможно, потому что это нарушает причинно-следственную связь выходного сигнала от входного.
Появление цифровой техники в целом и цифровых источников сигналов в частности позволило избавиться от недостатков аналоговых фильтров путём реализации их непосредственно программным образом, в цифре. Такой подход требует «мультиампинг» — когда используется отдельный усилитель мощности для каждой полосы частот — в отличие от классического подхода, когда сначала усиливается широкополосный сигнал, который разбивается на частотные полосы (обычно) пассивными фильтрами. Применение нескольких усилителей вместо одного очевидным образом удорожает технику, поэтому такое решение выбирают для особо качественных систем.
▍ Краткое введение в цифровые фильтры
Цифровой фильтр — это функция, которую можно рассматривать как во временной, так и в частотной области. Во временной области она определяет импульсную характеристику, получаемой при реакции некоторого устройства или его мат. модели на единичный импульс (на слух воспринимаемый как щелчок). В частотной области она определяет затухание или усиление амплитуды и сдвиг фазы на отдельно взятой частоте. Переход между этими областями (в англоязычной литературе используется слово domain) осуществляется через преобразование Фурье, которое между функциями во временной и в частотной области задаёт однозначное соответствие.
Разделяют два типа цифровых фильтров:
IIR (Infinite Impulse Response)
— фильтры с бесконечной импульсной характеристикой. По сути, представляют собой всё те же аналоговые фильтры, но «моделируемые» в цифре — математический аппарат в обоих случаях идентичен (в основе которого лежит преобразование Лапласа). Отсюда следует бесконечность импульсной характеристики, которую можно представить в виде суммы экспоненциально затухающих синусоид.
Вот так выглядит (обрезанная справа) импульсная характеристика рекурсивного фильтра низких частот с высокой добротностью
Их преимуществом является низкая вычислительная сложность — каждое новое значение вычисляется рекурсивно в зависимости от предыдущих. Они также чувствительны к погрешностям вычисления и ошибкам округления — поэтому вопрос устойчивости (гарантированного затухания при отсутствии сигнала на входе) таких фильтров в теории рассматривается отдельно.
Наиболее простым является фильтр низких частот первого порядка:
FIR (Finite Impulse Response)
— фильтры с конечной импульсной характеристикой. Самый известный фильтр такого рода — это скользящее среднее, а сама фильтрация осуществляется посредством линейной свёртки отсчётов фильтра с отсчётами входного сигнала. Здесь сложность уже квадратичная — однако её можно уменьшить до , если использовать алгоритм быстрой свёртки с использованием быстрого преобразования Фурье (FFT). Конечность количества отсчётов накладывает свои ограничения на форму АЧХ, приводя к пульсациям.
Примечание
На самом деле математически и IIR-фильтры, и FIR-фильтры описываются одинаково — через отношение полиномов. Разница в том, что у IIR-фильтров степень и у числителя, и знаменателя небольшая, а у FIR-фильтров высокая степень числителя компенсирует единичный знаменатель. Эта тема достаточно сложная и занимает немалую часть в теории обработки сигналов; для практических задач в неё углубляться не обязательно, интересующим же можно порекомендовать вспомнить про ряд Тейлора, затем перейти к производящей функции и уже после разбираться с z-преобразованием.
А так выглядит импульсная характеристика фазолинейного FIR-фильтра низких частот
Довольно популярной практикой при проектировании фильтров является линеаризация — когда берётся АЧХ известного IIR фильтра и формируется из неё FIR с линейной фазой.
Снова о простом активном фильтре для АС
Цитата: Chugunov
Забавная ситуация — люди ловят сотки в симуляторах,….далее по тексту
Приветствую Сергей!!! Согласитесь, что сейчас Вы написали много неабсолютных истин. Вот смотрите: Судя по всему, в первоначальной схеме динамики должны включаться в противофазе (почему-то я забыл про такую возможность и добивался согласования при синфазном включении). -Это касается только согласования по фазе напряжения на выходе фильтра. А как там будет с реальными динамиками, еще вопрос.
Забавная ситуация — люди ловят сотки в симуляторах, забывая о том, что работают не отдельно фильтры, а целая система: фильтры, усилитель, акустика. Получается, как у Райкина: «к пуговицам претензии есть?». Умалчивают, что в симуляторах считается, что динамики идеальные (сферический конь в вакууме) или по крайней мере все динамики перекрывают с хорошей линейностью частоту раздела на две октавы (ха ха ха). -Нет никакого смысла даже к кривым динам лепить кривой фильтр, изначально. Симулятор не панацея, и никто особо блох не ловит.Просто намного проще все это прикинуть, чтобы избежать явных ошибок. На мой взгляд, обязательна подстройка измерительным микрофоном фильтров на всей системе со штатными усилителями и акустикой, иначе, к пуговицам претензий не будет, а в целом… -это уже потом, а сначала бы желательно сделать работоспособное все остальное. А потом уже доводка.
Думаю, любые фильтры — зло. -Не знаю попробуйте обойтись. Проблема выбора заключается в том, как выбрать наименьшее общее зло. -С этим не поспорю. Это филосовский вопрос. Из теории известно, что чем круче АЧХ фильтров, тем хуже их ФЧХ. Наверное, надо (при стремлении к совершенству) испробовать разные варианты. -Это в какой теории?? И как ФЧХ фильтров может быть хуже или лучше? ФЧХ фильтров ( по напряжению просто наклонная линия с той или иной степенью наклона). Другое дел суммарная ФЧХ 2-х или трех фильтров , работающих совместно на одну нагрузку. Так так и надо говорить. А известно ли, что ФЧХ еще не все? У фильтров 1-го порядка тоже масса недостатков, например направленность на частоте раздела дико кривая ( по сравнению с фильтрами четных порядков повыше). А это не в меньшей степени влияет на качество.
Думаю, наибольший положительный эффект от активных фильтров будет для систем среднего уровня (коих абсолютное большинство). Думаю, данный фильтр имеет полное право на существование и повысит качество и возможности большинства систем. — В активной акустике Женелек активные фильтры. И она очень высокого класса. P.S. Забавно, что прогрэссивная блочная система с принципом «любой усилитель подключаем к любым колонкам» сегодня выходит боком. Раньше, покупая приличную звуковую систему, включающую усилители и акустику, мы имели оптимизированные для совместной работы звенья, которые гарантированно хорошо работали. Сегодня можно кубить отдельные дорогие кубики, которые будут неважно работать вместе. -Никто и никогда не говорил, что «кубики» универсальны. Только до какой то степени и при правильном подборе. Всегда аппаратура подбирается друг к другу, это было есть и будет. Даже то, что было все в одном и настроено на заводе может и не звучать в плохом помещении. И не вся техника раньше конструировалась и настраивалась с любовью, ой не вся.
▍ Постановка задачи
Итак, нашей задачей является сформировать пару фильтров, делящих полосу частот на две с перекрытием. При этом они должны обладать следующими характеристиками:
- Гладкая АЧХ без пульсаций;
- Фазолинейность (сдвиг фаз на всех частотах равен нулю);
- Симметричность АЧХ в логарифмическом масштабе частот.
Примечание
пункт 1) означает, что мы не закладываем в фильтр пульсации так, как это делается, например, в фильтре Чебышёва. В теории, идеально гладкая АЧХ доступна только в IIR-фильтре бесконечной длины. На практике нам достаточно лишь, чтобы уровень пульсаций не превышал уровень шума входного сигнала, который для аудио-сигналов составляет -120 дБ в целом и -90 дБ для компакт-дисков и прочих 16-битных записей.
Cимметричность (зеркальность) АЧХ решает две задачи: 1) ВЧ-составляющую сигнала можно получить вычитанием из исходного НЧ-составляющей — как в частотной, так и во временной области; 2) избавляет от мучительного выбора, для какого фильтра — НЧ или ВЧ — предпочтительнее более пологий или крутой спад АЧХ.
Похожее требование есть у квадратурных зеркальных фильтров, в которых задаётся симметрия в линейном масштабе частот. Но нас интересует именно логарифмический масштаб, как более естественный для человеческого слуха.
Кроме того,
стиль изложения в описании квадратурных зеркальных фильтров что в википедии, что в типичных научных работах мало способствует понимаю того, как их нужно реализовывать на практике даже не очень далёкому от математики программисту.
Проект «трехполоски» и влияние деталей в фильтре АС
Январь, благодаря праздникам, оказался плодотворным для творчества — я закончил свой проект «трехполоски», растянувшийся на несколько лет. Хочу поделиться итогами и предлагаю обсудить два важны момента: трудности в организации места для прослушивания и о влиянии деталей в фильтре АС.
У меня довольно сложные акустические условия и нет отдельной комнаты для прослушивания. Был совсем не уверен, что получится, но «старшие товарищи» помогли ценным советом и рекомендациями в выборе головок, за что им очень благодарен. Именно поэтому выбор головок не случаен.
Morel 328 + ScanSpeak D7608 — проверенная связка, а Wavecor WF182BD мне нравится за низкие искажения. Результат оказался предсказуем и времени на создание АС было потрачено относительно не много. Корпус – МДФ в белом лаке, три полосы, фазоинвертор, вес 42 кг (каждая). Звучание очень открытое, масштабное. Баса не очень много, но я и не ставил задачу получения громоподобного низа, важнее другое — с комнатой АС «подружить». Думаю, что и в относительно большом помещении они будут комфортно звучать. Одно из достоинств в этом проекте — середина. И она очень хороша.
Я и раньше слышал купольные СЧ головки, поэтому было желание использовать именно эти головки. Еще было условие, что акустику невозможно выставить на слушателя, АС вынуждены стоять строго параллельно. В общем, решил пойти довольно непредсказуемым путем — использование в трехполосной системе не одного большого динамика, а двух относительно небольших. Думаю, что именно такое расположение головок, по вертикали сравнительно низко от пола, позволяет решать вопросы сложного для акустики помещения.
Много времени уделил внешнему виду. Решил выбрать белый цвет, чтобы акустика не выглядела огромной и даже в выключенном состоянии радовала своим видом. В итоге получился вот такой проект с «неправильной» расстановкой АС в сложной комнате. Еще жду шипы, возможно плиты подложу. Но главное — джаз, старый рок и вокал звучат очень хорошо.
АЧХ с 1 м. без сглаживания (нам ведь нужна правда) и импеданс
Теперь хотел поговорить о влиянии конденсаторов и катушек в фильтре. Ранее уже писал, что делал в макетном корпусе проект на головках морель CAW 638 и ET 338. В настоящий момент все это собрано в «презентабельный» корпус и в фильтре на ВЧ-головку установил MKP Mundorf MCap Supreme, вместо ранее использованного белого MKP Mundorf MCap, а на нч-сч установлена катушка индуктивности Mundorf M-Coil CF CFC16 17 mm.
Результат использования таких деталей очень хорошо слышно. А вот контрольные замеры АЧХ, импеданса не обнаружили изменения. Но саксофон, вокал приобрели новые «штрихи», можно сказать, что стали более осязаемые, повысилась «телесность, контрастность» образов. С.Жилин зазвучал новыми оттенками, именно на его композициях проявилась какая-то многогранность, которая ранее не была заметна. Честно сказать не ожидал таких изменений в звуке. Я и ранее пробовал Mundorf MCap Supreme с ET 308, но именно с ET 338 это проявилось столь отчетливо. А катушки из фольги ранее не приходилось использовать и сравнить не могу с другими НЧ/СЧ-головками. Думаю, что такого рода премиальные катушки и конденсаторы способны раскрыть способности головок очень высокого уровня. Но, с относительно бюджетными, это может быть и не заметно.
▍ Общий алгоритм построения
Существует несколько подходов к проектированию КИХ-фильтров, из которых наиболее простым и интуитивно-понятным является следующий:
- В частотном домене задаётся желаемая АЧХ фильтра;
- Производится обратное преобразование Фурье:
- Накладывается оконная функция.
Его можно выполнить как чисто аналитически, так и численно, используя дискретное преобразование Фурье (далее FFT). Аналитическое решение сложнее и имеет очевидное ограничение на использование только тех функций, для которых известны Фурье-образы.
▍ Аналитическое решение
Озвученным выше требованиям гладкости и симметрии (но не фазолинейности) соответствует фильтр Линквитца-Рейли. Зная формулу АЧХ , где — порядок фильтра, формулу импульсной характеристики можно получить аналитически через интеграл Фурье, а конкретные отсчёты FIR фильтра считать непосредственным её вычислением.
График фильтра в логарифмическом масштабе:
Лучший способ для вычисления интеграла Фурье — это использовать какую-нибудь систему компьютерной алгебры. Например, в Wolfram Mathematica это будет выглядеть так:
InverseFourierTransform[1/(1 + w^2), w, x] // FullSimplify ↓
График получившейся функции, она же импульсная характеристика:
Как видно из формулы и графика, импульсная характеристика бесконечна — стремится к нулю, но не достигает его; а также симметрична относительно нуля (за счёт фазолинейности). Ограничение её во времени осуществляется путём умножения на оконную функцию, за счёт чего значения функции за пределами окна приобретают нулевые значения, не требующих участия в расчётах. Побочным эффектом этого становится искажения исходного спектра фильтра — поскольку при умножении функций их спектры сворачиваются. Итоговый спектр можно увидеть также через преобразование Фурье. Например, для прямоугольного окна получим
в результате чего АЧХ фильтра изменится на
код
FourierTransform[E^-Abs[x] Sqrt[Pi/2] UnitBox[x/5], x, w] // FullSimplify ↓
Пульсации, которые мы видим, являются следствием от наличия «боковых лепестков» оконной функции. Их можно уменьшить, взяв более гладкое и широкое окно. Среди множества разработанных окон одним из наиболее оптимальных и удобным для аналитических вычислений является окно Нуттала, определяемое как
Примечание
Используя полиномы Чебышёва, окно Нуттала также можно вычислить как , где
Помножив её на импульсную характеристику фильтра, получим:
а АЧХ примет вид
код
frnw = FourierTransform[E^-Abs[x] Sqrt[Pi/2] NuttallWindow[x/20], x, w] // Simplify ↓
Как видно, величина пульсаций значительно уменьшилась. По графику видно, что «полка» фильтра слегка опустилась — в идеале это тоже нужно учитывать и компенсировать. В данном случае она составила (на нулевой частоте):
FourierTransform[E^-Abs[x] Sqrt[Pi/2] NuttallWindow[x/20], x, w] /.w->0.0 ↓
Мнимая часть здесь получилась вследствие погрешности при численных вычислениях и её можно смело отбрасывать (об этом говорит значение , поскольку точность вычислений в формате double и представляет примерно 16 десятичных цифр).
Аналогичным образом можно посчитать импульсные характеристики и для более высоких (но только целых) порядков, например:
InverseFourierTransform[1/(1+w^4), w, x] // FullSimplify ↓
Как видно, автоматического упрощения уже недостаточно и здесь требуется ручная работа по приведению формулы к удобочитаемому виду. В итоге получается следующая формула (в комплексных числах) для импульсной характеристики фильтра Линквитца-Рейли произвольного порядка:
При вычислении за счёт сложения комплексно-сопряжённых чисел мнимая часть обнуляется и в результате получится чисто действительная функция. Эту формулу можно выписать и непосредственно в действительных числах:
Акустика компьютерных колонок
Довелось посмотреть на Ютуб видео: юноша объявил, что сделает акустическую систему своими руками. Отрок талантлив: раскурочил колонки персонального компьютера — ну, совсем никакие — извлек на свет Божий усилитель с регулятором, поместил в спичечный коробок (корпус акустической системы). Компьютерные динамики известны плохим воспроизведением низких частот. Сами устройства маленькие, легкие, во-вторых, буржуи материалами экономят. Откуда в акустической системе взяться басам. Юноша взял… читайте дальше!
Наидорожайший компонент музыкального центра. Акустика класса hi-end стоимостью обходит дешевую квартиру. Ремонт, сборка колонок неплохой бизнес.
Усилитель низкой частоты акустической системы соберет продвинутый радиолюбитель, никаких кулибиных не нужно. Из спичечного коробка торчит ручка регулятора громкости, вход с одной стороны, выход — с другой. Динамики старой акустической системы малы. Юноша раздобыл старенький громкоговоритель не сказочных размеров, но солидный. С колонки советских времен акустической системы.
Чтобы звук не тревожил воздух пищанием, умный отрок сколотил дюймовые доски ящиком. Динамик старенькой акустической системы поместил в размеров почтовой коробки, сместил, как это делается производителями современных сабвуферах домашних кинотеатров. Изнутри колонку звукоизолятором отделывать поленился. Желающий может использовать для акустической системы ватин, другой схожий материал. Маленькие динамики помещены вовнутрь продолговатых коробок, только-только вмещающих торцом громкоговоритель. Гордый отрок подключил один канал акустической системы на два маленьких динамика, второй — на один большой. Работает.
Юноша сказочный молодец, не пьет в подворотне, уподобляясь сверстникам, не портит в свободное время будущих невест, занят делом. Как говорил один знакомый: «Молодому поколению прощается недостаток знания и опыта, не избыток наглости, упроченного равнодушием».
Улучшения
Решили усовершенствовать методику, откровенно надеемся, дополнение поможет сделать акустическую систему самостоятельно несколько качественнее. Проблема? Понятие выдумано радиотехниками, создателями акустических систем – частота. Вибрация Вселенной имеет частоту. Говорят, даже ауре человека присуще. Каждая добротная колонка недаром вмещает несколько динамиков. Большие предназначены для низких частот, басов; прочие – для средних и высоких. Не только размер, а и устройство у них разное. Мы уже обсуждали этот вопрос и интересующихся отсылаем к написанным обзорам, где приводится классификация акустических систем, раскрываются принципы действия наиболее популярных.
Компьютерщикам известен системный зуммер, работающий по прерыванию BIOS, который способен вроде бы выдавать один звук, но талантливые программисты выписывали на нем вычурные мелодии, даже с попыткой цифрового синтеза и воспроизведения голоса. Однако при желании бас такая пищалка выдать не может.
К чему этот разговор… Большой динамик следовало бы не просто приспособить на один из каналов, а присудить специализацию басов. Как известно, большинство современных композиций (Звук Вокруг не берем) рассчитаны на два канала (стереовоспроизведение). Получается, что два одинаковых динамика (маленьких) играют одни и те же ноты, смысл в этом маленький. В то же время с этого же канала бас теряется, а высокие частоты гибнут на большом динамике. Как быть? Предлагаем внедрить в схему пассивные полосовые фильтры, которые помогут разбить поток на две части. Схему берем иностранного издания по той простой причине, что она первой попалась на глаза. Вот ссылка на исходный сайт chegdomyn.narod.ru. Радиолюбитель переснял из книги, приносим извинения автору, что не указываем первоисточник. Это происходит по той простой причине, что он нам не известен.
Итак, картинка. Бросаются сразу в глаза слова Woofer и Tweeter. Как не сложно догадаться, это, соответственно, сабвуфер для низких частот, и динамик для высоких. Охватывается диапазон музыкальных произведений 50-20000 Гц, причем на сабвуфер приходится полоса нижних частот. Радиолюбители могут сами по известным формулам просчитать полосы пропускания, для сравнения ля первой октавы, как известно, составляет 440 Гц. Считаем, что для нашего случая такое деление подойдет. Вот только хотелось бы найти два больших динамика, по одному на каждый канал. Смотрим схему…
Не совсем музыкальная схема. В положении, занимаемом системой, идет фильтрация голоса. Диапазон 300-3000 Гц. Переключатель подписан Narrow, переводится, как полоса. Чтобы получить Wide (широкое) воспроизведение, опускаем клеммы. Поклонники музыки могут выкинуть полосовой фильтр Narrow, любителям бороздить скайп рекомендуем избегать поспешного решения. Схеме напрочь исключит петлевой эффект микрофона, известный повсеместно: пронзительное гудение вследствие переусиления (положительной обратной связи). Ценный эффект, даже военный знает сложности использования громкой связи. Владелец ноутбука осведомлен…
Для устранения эффекта обратной связи изучите вопрос, найдите, на какой частоте резонирует система, отрежьте лишнее фильтром. Очень удобно. Касательно популярной музыки микрофон отключаем, уносим подальше от динамиков (случай караоке), начинаем петь. Фильтры верхних и нижних частот оставим неизменными, изделия просчитаны неизвестными западными друзьями. Испытывающим затруднения, читая иностранные чертежи, поясняем, схема изображает (полосовой фильтр Narrow отброшен):
- Емкость 4 мкФ.
- Неиндуктивные сопротивления R1, R2 номиналом 2,4 Ом, 20 Ом.
- Индуктивность (катушка) 0,27 мГн.
- Сопротивление R3 8 Ом.
- Конденсатор С4 17 мкФ.
Динамики должны соответствовать. Советы указанного сайта. Сабвуфером пойдет МСМ 1853, пищалкой (слово не списали) послужит РЕ 270-175. Полосы пропускания посчитаете самостоятельно. Большая буква Ω означает кОмы – ничего страшного нет, поменяйте номинал. Напоминаем, емкости параллельно соединенных конденсаторов складываются, как последовательно включенные резисторы. На случай, если сложно достать подходящие номиналы. Вряд ли получится изготовить динамики своими руками, набрать небольшие номиналы сопротивлений реально. Не используйте катушки, вырезаем пластины нихрома, подобных сплавов. После изготовления резистор лакируется, большого тока не планируется, защищать элемент не следует.
Индуктивности проще намотать самостоятельно. Логично использовать онлайн-калькулятор, задав емкость, получим параметры: количество витков, диаметр, материал сердечника, толщину жилы. Приведем пример, избегая быть голословными. Посещаем Яндекс, набираем нечто вроде «онлайн калькулятор индуктивности». Получаем ряд ответов выдачи. Выбираем понравившийся сайт, начинаем думать, как намотать индуктивность акустической системы номиналом 0,27 мГн. Нам понравился сайт coil32.narod.ru, начнем работу.
Исходные сведения: индуктивность 0,27 мГн, диаметр каркаса 15 мм, проволока ПЭЛ 0,2, длиною намотки 40 миллиметров.
Сразу возникает вопрос, видя калькулятор, где взять номинальный диаметр изолированной проволоки… Потрудились, нашли на сайте servomotors.ru таблицу, взятую из справочника, которую приводим в обзоре, считайте на здоровье. Диаметр меди составляет 0,2 мм, изолированной жилы – 0,225 мм. Скармливаем смело величины калькулятору, вычисляя нужные величины.
Получилась двухслойная катушка, числом витков 226. Длина провода составила 10,88 метра сопротивлением порядка 6-ти Ом. Главные параметры найдены, начинаем мотать. Самодельная акустическая система выполняется в ручной работы корпусе, примостить фильтр место найдется. К одному выходу подключаем пищалку, к другому – сабвуфер. Пару слов касательно усиления. Может статься, каскад усилителя не потянет четыре динамика. Каждая схема охарактеризована некой нагрузочной способностью, выше нельзя подпрыгнуть. Устройство акустической системы рассчитано, учитывая фиксированный запас, чтобы согласовать нагрузку, часто применяется эмиттерный повторитель. Каскад, заставляющий схему работать, полная отдача на любой динамик.
Напутствие начинающим конструкторам
Считаем, помогли читателям понять, как правильно конструировать акустическую систему. Пассивные элементы (конденсаторы, резисторы, катушки индуктивности) сможет достать, изготовить каждый. Осталось собрать корпус акустической системы своими руками. А за этим, верим, дело не станет. Важно понять, музыка сформирована гаммой частот, обрезаемых неправильным изготовлением устройства. Собравшись сделать акустическую систему, подумайте над этим, поищите компоненты. Важно передать великолепие мелодии, будет твердая уверенность: труд не пропал даром. Акустическая система прослужит долго, радость подарит.
Верим, изготовление акустических систем своими руками читателям будет в удовольствие. Грядущее время уникально. Поверьте, в начале XX века нельзя было черпать информацию тоннами ежедневно. Обучение выливалось тяжким кропотливым трудом. Приходилось обшаривать пыльные полки библиотек. Возрадуйтесь интернету. Страдивари пропитывал древесину скрипок уникальным составом. Скрипачи современности продолжают выбирать итальянские экземпляры. Вдумайтесь, прошло 30 лет, воз остался позади.
Нынешнему поколению известны марки клеев, наименования материалов. Необходимое продается магазинами. СССР лишил изобилия людей, снабдив относительной стабильностью. Сегодня преимущество описывается возможностью изобретения уникальных способов заработка. Профессионал-самоучка везде срубит капусты.
▍ Переход в дискретную область
Синтез фильтра в дискретном виде осуществляется сходным образом. Принципиальное отличие состоит в том, что:
- Частотный диапазон фильтра ограничен частотой дискретизации по определению;
- На выходе мы получаем периодический сигнал — в отличие от аналитического решения, в которой функция во времени затухает к бесконечности. Этот момент особенно важен, когда проектируются фазосдвигающие фильтры. Из этого также следует, что даже если мы не будем явно накладывать оконную функцию, по факту у нас в любом случае будет наложено прямоугольное окно.
Попробуем реализовать тот же фильтр НЧ. Первым делом необходимо определиться с частотой дискретизации и размером массива. Размер массива ограничивает нижнюю частоту фильтра (но не постоянную составляющую). Если не ставить задачей минимизацию размера, то 2048 отсчётов обычно достаточно. Размер выбирается кратным степени двойки исходя из ограничений стандартной реализации БПФ.
Примечание
Быстрые алгоритмы существуют и для степеней тройки, и для взаимно простых чисел, и для некоторых других частных случаев — но для степеней двойки, четвёрки и восьмёрки они наиболее быстрые.
Также имеются различия (но не результат) при работе с классическим (комплексным) FFT, Real-FFT, который работает только с половиной спектра, предполагая его симметрию, и FHT (быстрое преобразование Хартли), в котором изначально и данные, и спектр определены в поле действительных чисел. Здесь будет использоваться классический FFT.
Итак, определим формулу для фильтра — для примера 4-го порядка:
FilterAmps[w_] := 1/(1+w^8);
Выберем частоту дискретизации (в герцах), стандартную для современных ЦАП:
samplerate = 48000;
Выберем частоту среза, на которой подавления будет составлять 0.5 (-6 дБ) и соответствовать нормированной частоте w=1:
fc = 1000;
Выберем размер массива (маленький, для наглядности):
size = 128;
Далее необходимо заполнить массив. Каждому элементу в нём будет соответствовать частота от 0 (постоянная составляющая) до (частота Найквиста), равномерно распределённых в линейном масштабе. Определим функцию, которая в зависимости от индекса будет считать нормированную частоту:
w[index_] := (index*samplerate)/(size*fc)
Заполняем первую половину (положительную часть спектра) массива:
halfspectrumdata = Table[FilterAmps[w[index]]*(-1)^index, {index, 0, size/2}];
Здесь фазу на каждой нечётной частоте мы повернули на 180° для того чтобы после БПФ максимум импульса был расположен по центру массива.
Вторую половину (отрицательную часть спектра) получаем реверсом первой, за исключением крайних частот (нулевой — постоянной составляющей и максимальной — частоты Найквиста, потому что для их описания достаточно одного числа).
spectrumdata = Join[halfspectrumdata, Reverse[halfspectrumdata[[2;;size/2]]]];
Получили следующее:
Теперь делаем обратное преобразование Фурье:
wavedata = InverseFourier[spectrumdata];
И накладываем оконную функцию — Нутталла, как и в прошлый раз:
В качестве заключительного аккорда можно нормировать полку фильтра к единице. Для этого снова потребуется прямое FFT, чтобы узнать значение постоянной составляющей:
Fourier[wavedata][[1]] ↓
и затем просто поделить на него значение каждого отсчёта в импульсе
wavedata /= Fourier[wavedata][[1]];
Сделав FFT ещё раз, можно убедиться, что постоянная составляющая стала равной единице:
Fourier[wavedata][[1]] ↓
Если бы мы проектировали фильтр высоких частот, но нормализацию нужно было бы делать по амплитуде не на нулевой частоте, а на частоте Найквиста.
Проектирование акустики
Изначально выбираем количество колонок, тип, местоположение. Очевидно, изготавливать в большем числе, нежели имеет каналов домашний кинотеатр, неразумный тактический ход. Кассетному магнитофону хватит двух колонок. К домашнему кинотеатру выйдет уже не менее шести корпусов (динамиков будет больше). Согласно потребностям аксессуары встраиваются в мебель, качество воспроизведения низких частот хромает. Теперь вопрос выбора динамиков: в издании авторства Найденко, Карпова приведена номенклатура:
Трехполосная акустическая система
- Низкие частоты – головка CA21RE (H397) посадкой на 8 дюймов.
- Средний диапазон – головка MP14RCY/P (H522) на 5 дюймов.
- Верхние частоты – головка 27TDC (H1149) на 27 мм.
Приводили базовые принципы конструирования акустических систем, предлагали электрическую схему фильтра, рассекающего поток на две части (выше дан перечень трех поддиапазонов), приводили название покупных динамиков, решающих задачу создания двух колонок стерео. Избегаем повторяться, читатели могут взять труд полистать раздел, найти конкретные названия.
Следующим вопросом будет фильтр. Полагаем, фирма National Semiconductor не обидится, если отскриним чертеж усилителя перевода Ридико. Рисунок показывает активный фильтр с питанием +15, -15 вольт, 5 однотипных микросхем (операционных усилителей), граничная частота поддиапазонов вычисляется формулой, приведенной на изображении (дублируем текстом):
f = 1 / 2П RC;
П – число Пи, известное школьникам (3,14); R, C – номиналы резистора, емкости. На рисунке R = 24 кОм, С – замалчивается.
Активный фильтр, питаемый электрическим током
Учитывая возможности выбранных динамиков, читатель сможет подобрать параметр. Берутся характеристики полосы воспроизведения колонки, находится стык перекрытия между ними, туда выносится граничная частота. Благодаря формуле, вычисляем величину емкости. Номинал сопротивления избегайте трогать, причина: может (спорный факт) задавать рабочую точку усилителя, коэффициент передачи. На частотной характеристике, приведенной в переводе, которую опускаем, граница составляет 1 кГц. Давайте посчитаем емкость указанного случая:
С = 1 / 2П Rf = 1 / 2 х 3,14 х 24000 х 1000 = 6,6 пФ.
Не ахти какая большая емкость, выбирается из условия максимально допустимого напряжения. В схеме с источниками +15 и -15 В вряд ли стоит номинал, превышающий суммарный уровень (30 вольт), возьмите пробивное напряжение (справочник поможет) не менее 50 вольт. Не пытайтесь поставить электролитические конденсаторы постоянного тока, схема обретает шансы взлететь на воздух. Отсутствует смысл разыскивать исходную схему чипа LM833 по причине Сизифова труда. Некоторые читатели найдут замену микросхеме, отличающуюся… надеемся на понимание.
Насчет сравнительно небольшой емкости конденсаторов (рознично и суммарной) описание фильтра говорит: благодаря низкому импедансу головок без активных компонентов номиналы пришлось бы увеличить. Закономерно вызывая появление искажений, обусловленных наличием электролитических конденсаторов, катушек с ферромагнитным сердечником. Не стесняйтесь двигать границу деления диапазонов, общая пропускная способность остается прежней.
Пассивные фильтры акустической системы
Пассивные фильтры соберет своими руками каждый обученный пайке, курс школьной физики. В крайнем случае заручитесь помощью Гоноровского, лучше некуда расписаны тонкости прохождения сигналов через радиоэлектронные линии, обладающие нелинейными свойствами. Приведенный материал заинтересовал авторов фильтрами низкой и высокой частоты. Желающие поделить сигнал на три части должны зачитываться трудами, раскрывающими базис полосовых фильтров. Максимально допустимое (или пробивное) напряжение выйдет мизерным, номинал станет значительным. Под стать упомянутым электролитическим конденсаторам емкости номиналом десятки микрофарад (три порядка выше используемых активным фильтром).
Новичков тревожит вопрос получения напряжения +15, -15 В питания акустических систем. Намотайте трансформатор (пример приводился, программа ПК Trans50Hz), снабдите двухполупериодным выпрямителем (диодный мост), профильтруйте, наслаждайтесь. Наконец, активный или пассивный фильтр прикупите. Называется указанная вещица кроссовером, внимательно подбирайте динамики, диапазоны точнее соотносите с параметрами фильтра.
Для пассивных кроссоверов акустических систем найдете в интернете множество калькуляторов (https://ccs.exl.info/calc_cr.html). Исходными цифрами программа расчета принимает входные сопротивления динамиков, частоту деления. Введите данные, программа-робот быстро снабдит величинами емкостей и индуктивностей. На приведенной страничке задавайте тип фильтра (Бесселя, Баттерворта, Линквица-Райли). На наш взгляд задачка для профи. Приведенный выше активный каскад образован фильтрами Баттерворта 2-го порядка (скорость снижения АЧХ 12 дБ на октаву). Касается частотной (АЧХ) характеристики системы, понятно только профессионалам. Если сомневаетесь, выбирайте золотую серединку. В прямом смысле ставьте галку на третьем кружке (Бессель).
▍ Кусочно-непрерывные фильтры
Исходя из изначально поставленной задачи, описывать АЧХ удобнее кусочно-непрерывной функцией, в которой полосы пропускания и подавления константны и равны 1 и 0 соответственно, заданной в логарифмическом масштабе. Выводу таких функций была посвящена отдельная статья, здесь для примера мы возьмём стандартную smooth-step функцию, построенной из кубического полинома 3-го порядка: Из её графика в линейном масштабе симметрия, обеспечивающая суммирование в единицу, хорошо видна:
А вот в логарифмическом масштабе — уже нет, зато хорошо видно главное отличие от фильтра Линквитца-Рейли — спад не пологий, а имеет выраженную границу справа, за которой громкость (в децибелах) равна минус бесконечности. Дополнение до единицы даёт ВЧ-фильтр (жёлтым цветом), который и обладает желаемой симметрией:
На большем диапазоне громкости это свойство фильтров выглядит ещё более наглядным:
В отличие от классических фильтров, где параметризация крутизны спада АЧХ через порядок обусловлена их схемотехнической реализацией, здесь мы можем оперировать непосредственно шириной полосы сопряжения, задавая её в октавах от частоты раздела в -6 дБ. Для этого потребуется дополнительная функция для перевода логарифмического масштаба в линейный, значение которой будет передаваться в smooth-step функцию для определения амплитуды на частоте . Её можно определить несколькими путями:
1) через граничные частоты
2) через центральную частоту и ширину (в октавах)
3) через центральную и верхнюю граничную частоту
4) через центральную и нижнюю граничную частоту
Теперь, используя некоторую функцию фильтра, можно получить его импульсную характеристику по вышеописанному алгоритму, который можно определить отдельной функцией:
SymmetricFilterImpulseResponse[f0_, width_, size_, samplerate_, ClipFunction_, WindowFunction_] := Table[ClipFunction[(2 Log[(index samplerate)/(f0 size)])/ (width Log[2]) ] (-1)^index, {index, 0, size/2}] // Join[#, Reverse[#[[2 ;; size/2]]]] & // InverseFourier[#] Table[WindowFunction[(index-1)/size-1/2], {index, 1, size}] & // #/ Fourier[#, FourierParameters -> {1, -1}][[1]] & // Re
Примечание
В разных реализациях свёртки через ДПФ существуют разные подходы к нормализации импульсной характеристики по амплитуде. Здесь она делается не отдельной операцией, а заданием опции FourierParameters при выполнении ДПФ.
Передав в эту функцию наш кубический фильтр и окно Нуттала получим
SymmetricFilterImpulseResponse[1000, 0.5, 512, 48000, FilterCubicClip, NuttallWindow] ↓
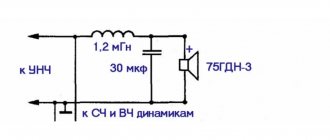
Фильтр для низкочастотного динамика
Фильтр нижних частот из дросселя и конденсатора большой ёмкости называется схемой Баттерворта второго порядка. Он обеспечивает спад частот выше частоты среза до 12 dBна октаву. Схема работает следующим образом. Индуктивность в LC контуре выполняет функцию переменного резистора. Его сопротивление прямо пропорционально частоте ивозрастает с увеличением диапазона. Поэтому высокие частоты практически не попадают на НЧ динамик. Такую же функцию выполняет и конденсатор. Его сопротивление обратно пропорционально частоте и он включается параллельно громкоговорителю.
Поскольку схема устройства должна хорошо пропускать низкие частоты и обрезать высокие, то конденсаторы такого устройства имеют большую ёмкость.Пассивный фильтр для динамика может быть выполнен по более сложной схеме. Если соединить две схемы Баттерворта последовательно, то получится устройство четвёртого порядка из двух индуктивностей и двух конденсаторов. Оно обеспечивает спад частотной характеристики низкочастотного громкоговорителя в 24 децибела на октаву.
Для того чтобы выровнять частотную характеристику и более точно согласовать схему Баттерворта и динамик, между катушкой индуктивности и конденсатором, включается резистор с небольшим сопротивлением. Для этой цели лучше использовать проволочные резисторы.
▍ Несколько интересных фильтр-функций
Помимо уже рассмотренной кубической, можно придумать множество и других функций для фильтров, основанных на какой-нибудь математической идее. Также имеет значение, насколько легко может быть вычислена (и может ли быть вычислена вообще) обратная функция.
Параболическая, наименее вычислительно затратная. При необходимости, обратная к ней функция находится довольно элементарно:
Кубическая. Обратная к ней функция уже немного контринтуитивна (а если вам интересно, откуда здесь взялись тригонометрические функции — тогда сюда):
Используя полином 5-ой степени, с двумя нулевыми производными на границах сопряжения. Обратная функция здесь уже в элементарных функциях не выражается (потому и не приведена):
Используя полином 13-ой степени — с дополнительным «выпрямлением»:
Используя рациональный полином — даёт более гладкую характеристику и более простую обратную функцию, чем у кубической:
С заданным количеством нулевых производных в точках стыковки, частным случаем которой является предыдущая функция. Обратная к ней функция также легко находится:
Линейно спадающая в логарифмическом масштабе:
Более плавный вариант предыдущего с возможностью регулировки «жёсткости». Здесь уже обратная функция для произвольного n в элементарных функциях не выражается:
С бесконечным количеством нулевых производных в точках стыковки, что обеспечивает идеальное сопряжение. А здесь обратная функция легко находится:
С максимально быстро затухающей импульсной характеристикой — что при достаточно больших () позволяет обойтись без оконной функции вообще. Сама формула получена модуляцией аргумента кубической функции, т.е. :
Здесь — это специальная функция (функция ошибок), определяемая как интеграл от гауссианы. Вместо неё можно использовать функцию гиперболического тангенса — импульсная характеристика также будет достаточно быстро затухать, хоть и не так быстро, как в предыдущем случае. Причём при больших n визуально она будет походить на Линквитца-Рейли и это совсем не случайно —
потому что
Сделав в функции замену и сократив, получим не что иное, как