Sampling frequency
(or
sampling rate
, English
sample rate
) - the sampling frequency of a time-continuous signal when it is sampled (in particular, by an analog-to-digital converter). It is measured in Hertz.
The term is also used for inverse, digital-to-analog conversion, especially if the sampling frequency of the forward and inverse conversion is chosen differently (This technique, also called “Time Scaling,” is found, for example, when analyzing ultra-low-frequency sounds made by marine animals).
The higher the sampling rate, the wider the spectrum of the signal that can be represented in the discrete signal. As follows from Kotelnikov's theorem, in order to uniquely restore the original signal, the sampling frequency must be more than twice the highest frequency in the signal spectrum.
Some of the audio sampling rates used [1]:
- 8,000 Hz - telephone, enough for speech, Nellymoser codec;
- 11,025 Hz - a quarter of an Audio CD, sufficient for speech transmission;
- 16,000 Hz;
- 22,050 Hz - half Audio CD, enough to transmit radio quality;
- 32,000 Hz;
- 44 100 Hz - used in Audio CD. Selected by Sony for reasons of compatibility with the PAL standard, due to the recording of 3 values per line of the frame image × 588 lines per frame × 25 frames per second, and sufficiency (according to Kotelnikov’s theorem) for high-quality coverage of the entire range of frequencies distinguishable by humans by ear (20 Hz - 20 KHz);
- 48,000 Hz - DVD, DAT;
- 96,000 Hz - DVD-Audio (MLP 5.1);
- 192,000 Hz - DVD-Audio (MLP 2.0);
- 2,822,400 Hz - SACD, a single-bit delta-sigma modulation process known as DSD - Direct Stream Digital, jointly developed by Sony and Philips;
- 5,644,800 Hz - Double sample rate DSD, one-bit Direct Stream Digital with twice the sample rate of SACD. Used in some professional DSD recorders.
What is Sample Rate (Sampling Rate)? What is bit depth?
When a signal enters the ADC from a preamplifier, compressor, console output, or synthesizer, it represents electromagnetic oscillations. That is, a certain wave with a changing voltage of very small values comes to the input of the ADC.
The result is a wave graph on a computer screen. Even the best converter has an error, because there are no intermediate values between zero and one, and the wave graph will consist only of vertical and horizontal segments, without inclined lines.
The graphical drawing of the wave will be influenced by the pitch of the sound, frequency of vibrations, its timbre, waveform and volume, amplitude. A high-quality ADC must correctly transmit all these parameters to the recording system. So, sound enters the system discretely, that is, divided into small sections. The accuracy of encoding an analog signal in a digital environment depends on the size of these segments. The smaller the horizontal and vertical discrete units, the more accurate the digitization.
The horizontal splitting of a wave gives us an idea of the sampling rate, or sampling rate. The more often the ADC records changes in wave graph values, the higher the sampling frequency. Actually, one sample is a discrete unit segment, a minimal unit of sound.
The shorter it is, the higher the sampling rate. For example, the value of the sampling frequency in Each sample is equal in duration to the previous one. For correct sound reproduction, the sample rates of the file and the system must be identical. When adding an audio track to a project with a sampling rate different from that of the host program, it must be converted. If you play a higher frequency file on a lower frequency system, it will sound slower than it should, and vice versa.
Why are some sounds beautiful and others not?
Here, for some reason, I’m tempted to take the gray volume of Feynman’s lectures and refresh my memories of Fourier series - but let’s keep it simple: any oscillation can be decomposed into several oscillations with shorter wavelengths. These smaller waves are the harmonics, and how many of them fit into the length of the main wave - two, three, etc. — determines whether they are even or odd. As it turns out, odd harmonics are perceived discomfortingly by our ears. And everything seems to be working correctly, but the discomfort remains.
A more obvious unpleasant sound is dissonance, two frequencies operating simultaneously and causing rare beats. If you want to see it even more clearly, press the nearby black and white keys on the piano.
There is also the opposite of dissonance - consonance. This is euphony itself, for example, an interval such as an octave (doubling the frequency), a fifth or a fourth. In addition, the comfort of sound is hampered by noises of various natures, distortions and overtones that mask it.
It is clear that noise is what interferes in principle. Sound garbage. However, there is also white noise, a kind of noise standard in which all frequencies (more precisely, spectral components) are uniformly present. If you want to move away from a source of white noise, it will turn pink as you move away. This happens because air more attenuates the higher frequencies of the audible spectrum. When there are fewer of them, then they talk about pink noise.
The louder the noise is in relation to the useful sound, the more that sound is masked by the noise. Comfort decreases, and then sound intelligibility decreases. The same applies to odd harmonics and nonlinear distortions, which we will talk about in more detail. All these phenomena are interconnected and, most importantly, they all prevent us from listening.
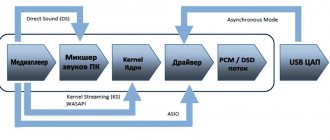
Digital audio path: upsampling and upscaling, WASAPI, ASIO and external master clock for USB audio
But this is just a guess. I have never come across a single device that did not support 48 kHz or did not recommend using 48 kHz for some reason. It’s clear that I’m still a long way from writing a game for the PlayStation, but that doesn’t matter. The main thing is that I found out that you need to work at 48 kHz. Don’t forget also that the oldfags care deeply about these high frequencies of yours. The auditory cochlea gradually dies with age, starting from the upper end, and a person loses range.
1.2. Kotelnikov's theorem (Nyquist Frequency)
Kotelnikov's theorem (better known in English literature as Nyquist Frequency) states that for correct transmission and subsequent reproduction of the entire frequency spectrum contained in the signal, the sampling frequency must be at least twice the highest frequency contained in the digitized signal. So that for each cycle of the highest frequency there are at least two amplitude measurements. That is, if we want the highest frequency perceived by human hearing (20 KHz) to be correctly reproduced, the required sampling frequency must be at least twice as high this frequency. So 20 KHz × 2 will equal 40 KHz. In mathematical form this is known as Nyquist's theorem and would look like this:
Dear visitor!
When a signal enters the ADC from a preamplifier, compressor, console output, or synthesizer, it represents electromagnetic oscillations. That is, a certain wave with a changing voltage of very small values comes to the input of the ADC. The result is a wave graph on a computer screen. Even the best converter has an error, because there are no intermediate values between zero and one, and the wave graph will consist only of vertical and horizontal segments, without inclined lines. The graphical drawing of the wave will be influenced by the pitch of the sound, frequency of vibrations, its timbre, waveform and volume, amplitude. A high-quality ADC must correctly transmit all these parameters to the recording system. So, sound enters the system discretely, that is, divided into small sections. The accuracy of encoding an analog signal in a digital environment depends on the size of these segments.
Note - the pitch of the sound and its frequency - depends on the specialty
In the understanding of sound, apparently, there are two extremes - the understanding of the sound engineer and the musician. The first one says "440 Hz!" the second is “note A!” And both are right. The first one says “frequency”, the second one says “pitch”. However, there are many excellent musicians who did not know sheet music at all. At the same time, no one has yet been able to meet specialists in the field of acoustics who do not know the physical foundations in this area.
It is important to understand that both of these specialists are engaged in comfortable sound in their own way. The author of a musical work, instinctively, or relying on conservatory knowledge, builds sound on the principles of harmony, avoiding dissonance or distortion. The designer who creates the speakers initially does not allow extraneous sounds, minimizes distortion, takes care of the uniformity of the amplitude-frequency response, dynamics and much, much more.
I’m writing an MP3 disc, which frequency is more profitable: 44.1 or 48?
A few words about the composition, operation and optimization of the digital audio path using a computer and USB. Basically, the topic is boring and there are a lot of letters, so if it’s difficult to master, go straight to the conclusions. An audio signal, in general, is encoded by a sequence of signal amplitude values measured at regular intervals.
Not only for beginners, but also for some enthusiasts who have been involved in sound for many years, it will seem like a revelation that the banal recording process is accompanied by the most complex physical phenomena. One of these is called discretization. By definition, it is the process of converting a continuous function into a discrete one. It is difficult for people far from science to understand this, especially since quantum physics is involved here - the most complex of those existing today. But professional sound engineers, for example, those working in the Moscow recording studio "Interval", know what the audio sampling frequency is and which is best applicable in certain cases. Why? Because the final quality of recorded music depends on this phenomenon. During the cassette-film period, these nuances were omitted due to limited technical equipment. But in today's high-tech digital world, audio sampling rate matters when creating music and presenting it to listeners.
Comparison of data transfer formats
As soon as you decide on the number and combination of inputs and outputs you need, then you can begin to select the data transmission format that is best suited to solve your specific problems.
The oldest of the six major formats (PCI, PCMCIA, USB 1.1, USB 2.0, Firewire 400 and Firewire 800) are PCI and PCMCIA , and, contrary to the skepticism of many people, I personally think these formats are quite strong. For laptop owners, a PCMCIA card will generally be the most compact solution, while for PC owners, a PCI sound card installed inside is the most common and proven option. In addition, nowadays internal conflicts between PCI cards are quite rare. It is very unlikely that you will be able to use three audio interfaces with USB or Firewire data transfer formats at the same time without them conflicting.
The advantage of USB and Firewire audio interfaces is that they can be easily transferred from one computer to another, which is very convenient for those who use both a laptop and a PC in their work. Such interfaces are also convenient for those who do not want to open the lid of their computer again, or for those people who no longer have free slots on the motherboard.
Another undeniable advantage of USB and Firewire audio interfaces is the ability “hot” turn on and off the device (without turning off the computer’s power). However, this advantage is not particularly important for musicians, because when the studio software is running, “hot-plugging” the audio interface will still do nothing, the sound card will not be detected in the studio program, and the program will need to be restarted. Well, turning off the audio interface before exiting the program can completely cause the computer to hang. Also, USB and Firewire audio interfaces can cause problems with assigning drivers in the studio program, as a result of which tracks assigned to one sound card, after hot-plugging the audio interface, may end up being assigned to another sound card.
Also, hot plugging Firewire . There is information that some musicians have had their Firewire ports burnt out either on a peripheral device or on a computer when they were hot-plugged. And while Firewire theoretically supports up to 63 simultaneously connected devices, and USB up to 127, musicians have discovered (at their own expense) that plugging more than a couple of devices into a single port leads to hardware conflicts.
Those who still choose USB/Firewire inevitably encounter opinions, rumors, comments and facts that completely mislead them. Some musicians believe that USB is completely unsuitable for transmitting audio and MIDI signals , but in my experience I cannot agree with this opinion. At the very beginning of USB, version 1.1 did have some problems with data transfer, but now, working with USB 2.0, I can say that data transfer is very reliable.
USB 2.0 has not firmly established itself in the audio interface market, since not many manufacturers have implemented its support in their products, but at one time the Edirol UA1000 proved the reliability of this format for transmitting multi-channel audio . However, if you want an external audio interface with support for 24-bit/96kHz and a large number of channels, then Firewire is the right choice.
Detailing of concepts
What is bit depth and sampling frequency, which is better? The answer to this question, despite the complexity of the nature of these phenomena, can be obtained. There is no need to study physics textbooks. Suffice it to remember that Soviet semi-underground sound engineers recording rock and other music determined these indicators on an intuitive level. Discretization is also called sampling. This definition is more understandable for musicians. Its frequency implies the intensity of the processes at the moment when the analog signal is converted to digital. These include data storage, conversion, and direct digitization.
The sampling rate is measured in hertz. The guideline in its study is Kotelnikov’s theorem. Its author reveals the essence of discretization. According to the theorem, it limits the intensity of the digitized signal to half its own value.
Sampling frequency. What is its significance for sound recording?
Time sampling is a process that is directly related to the conversion of an analog signal to a digital signal. Along with it, the data is quantized by amplitude. Time sampling means measuring a signal at the time of its entire transmission. One sample is taken as a unit. If this is not entirely clear in words, then with an example it looks more convincing. Let's say the discredit frequency is 44100 Hz - the same one that was used on audio CDs. This means that the signal is measured 44,100 times within one second.
An analog signal is always superior to a digital signal in its saturation. And its transformation is an inevitable loss in quality. The sampling frequency serves as a kind of guideline: the higher it is, the closer the digital sound quality is to analog. This is clearly visible in the list below. It shows which sound frequency is better. Studying it, you will see the direct relationship between sampling and track quality:
- 1. 8000 Hz. This frequency is typical for telephone conversations and speech recording on a voice recorder with a simple set of functions. Used on audio converted through the Nellymoser codec.
- 2. 22050 Hz is used in radio broadcasting.
- 3. 44100Hz. As mentioned above, this frequency is typical for Audio CD, and this indicator has long been identified with the highest level of quality. And today the format does not lose its position.
- 4. 48000 Hz. These are DAT and DVD formats, which replaced AUDIO.
- 5. 96000 – DVD-audio MLP-5.1.
- 6. 2822 400 Hz – high-tech SACD Super Audio format.
The list clearly indicates which sound frequency is best. In addition, technology does not stand still, and new formats are emerging. But before making far-reaching plans, you should take into account one very significant nuance. Its essence is simple: the higher the sampling frequency, the more difficult it is to achieve technologically. To do this you need:
- ensure high intensity transmission of digital streams. But this is not possible on every interface. And the more channels are involved in recording (and this is typical for musical ensembles), the more complicated the process;
- have a processor capable of performing powerful computing operations. But even in the most modern samples, the possibilities for obtaining ultra-high quality sound are limited;
- use computer equipment with a large amount of RAM for recording.
Considering the above information, it is not surprising that the sound frequency of 44100 Hz continues to be the most popular today. It has been satisfying even the most demanding quality requirements for decades, and at the same time there are all the technical capabilities to achieve it. The last factor is decisive both for ordinary users and for most recording studios. Even knowing which sound frequency is best, in order to achieve it, you need to take care of the technical equipment.
Volume, sound pressure - limits and guidelines
With volume it's not so simple. It's relative. Think for yourself, because absolute silence does not exist. That is, it exists in nature, but getting into such a place turns into torture - you begin to hear the pounding of your heart, the ringing in your ears - all the same, the silence disappears.
Therefore, sound pressure is measured relative to a certain zero level in decibels (dB). These are logarithmic units, because the logarithmic scale most closely matches the nature of hearing. If we delve a little deeper into the theory, we need to remember the empirically established law of psychophysiology by Weber-Fechner, which describes the work of the senses. According to this law, the intensity of the sensation of something is directly proportional to the logarithm of the intensity of the stimulus. In the case of sound, this is the amplitude (range) of vibrations.
And if we take the threshold of audibility as zero decibels (and this, we repeat, is not silence!), then the rustling of leaves gives 10 dB, a subway train - 100 dB, a fighter in afterburner - 125 dB, and not much less, by the way, was given by one girl, a prize-winner scream loudness competition in the USA. In a disco hall, the volume can reach 130 dB. This is despite the fact that 120 dB is already painful, and 180 can kill.
A difference of approximately six decibels is perceived by us as doubling the volume. Adding three decibels at a low frequency requires doubling the amplitude of the sound source, but not every listener notices this aurally! These are paradoxical, at first glance, data.
Everything seems fine, so what's wrong?
Let's start with frequencies that are multiples of the sampling frequency. At a frequency of 441 Hertz at our sampling frequency (44.1 kHz), there are 100 points per period. Well, there are no complaints here, the sine wave is ideal. If we increase the frequency by an order of magnitude, i.e. 10 times, then these same 100 points will form not 1, but 10 periods. And even in this case, a signal very similar to a sine wave will be generated.
But at frequency 22050, i.e. At the highest frequency that satisfies Kotelnikov’s theorem (at a sampling frequency of 44.1 kHz), there are 50 oscillation periods per 100 points.
These signals were generated in Audacity. And at first I got the impression that there were enough dots there, it’s just that the scale doesn’t allow me to see it and that’s why everything is so angular...
Well... let's zoom in and look at each period separately:
The frequency of 4410 Hz is quite a worthy sinusoid, which cannot be said about the frequency of 22050 Hz , with its two points per period. In fact, this is no longer a sinusoid, but a triangular signal.
Of course, in any real DAC, a low-pass filter is used at the output, which cuts off the high-frequency component and rounds this triangle. However, the higher the class of your audio device, the more noticeable the angularity of the sound will be.
For the sake of experimentation, you can try to generate signals of the same frequency but different shapes in Audcity. In triangular and rectangular shapes, due to their “angularity” and sharp fronts, additional harmonics arise, but a sine wave signal sounds much softer and more natural.
But even this is not the worst thing. Up to this point, signals with frequencies that are multiples of the sampling frequency were considered.
Bit depth
Bit depth determines the dynamic range. When sampling sound waves, specify the amplitude value that is closest to the original sound wave amplitude for each sample. Higher bit depth can provide more possible amplitude values, resulting in a wider dynamic range, lower reference noise, and higher accuracy.
| Bit depth | Quality level | Amplitude value | Dynamic range |
| 8 bit | Telephone | 256 | 48 dB |
| 16 bit | Audio CD | 65,536 | 96 dB |
| 24 bits | Audio DVD | 16,777,216 | 144 dB |
| 32 bit | optimal | 4,294,967,296 | 192 dB |
The higher the bit depth, the greater the dynamic range provided.