The main principle of a car subwoofer

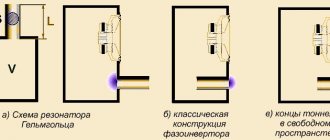
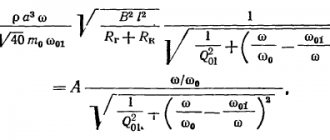
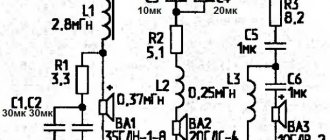
The last time we closely assessed the behavior of the speaker using the Thiel-Small parameters was several months ago; it’s time to “remember everything” on the second run, but we won’t. Let's remember just one key phrase.

Close to the text from “A3” No. 5/2005: “For midbass doomed to work in free-air conditions, the head parameters will be final, and for the subwoofer we use the head parameters for the calculation, according to which we make the design that is considered optimal.”

This means that we have smoothly and without fanfare moved on to operations with the subwoofer section of a car audio system, which we cannot do without. Either you can’t get by, or you don’t want to get by, or both. But before we get down to business, let’s ask the question for the sake of order: “And, actually, why?”

AND REALLY, WHY?

The question is partly sacrilegious, but let us remember: the most avid audiophiles (and those who simply like to listen to music who have joined them) can easily get by at home with speakers with low-frequency speakers of the caliber (using our terminology) of the same 6 - 7 inches that we have at the front, and feel great. By and large, there are two main reasons; it is not difficult to recall them again.

First: car doors are not at all equivalent to the powerful housings of home speakers, no matter what you do with them, and at the lowest frequencies the sound pressure drops. The midbass diffuser (if its frequency band is not forcibly limited in any way) desperately shakes, trying to portray bass, but they die in leaks and the softness of the thin steel shell, and only distortion becomes an audible result. They, as befits harmonics, are higher in frequency, therefore they are reproduced perfectly.

Second: in the car, music is listened to at higher volume levels, especially at low frequencies. This is due to both the incomparably higher level of external noise and simply tradition, which can outweigh any physical laws. How much do motorists like bass? In general, we know the answer: they love it very much. More precisely, in decibels?

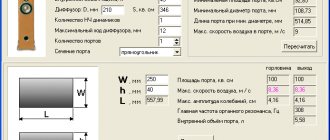
We obtain the dimensions of the body based on the known displacement

So, we come to the final stage of events. Now we need to calculate what geometric dimensions the bass reflex housing will have if its total displacement is known - 60.3 liters. We take measurements of the trunk, determining acceptable dimensions. For example, a structure 60 cm long and 40 cm high suits us. It remains to find out the width. Let’s decide that we will make the walls of the box from plywood 1.8 cm thick. Now we need to subtract the wall thickness from the length and height of the structure (1, 8x2) and get the following values: length – 56.4; height – 36.4 cm. Next we carry out the following calculations: 60.3x1000:36.4:56.4=29.4. This will be the width of the case, however, without taking into account the thickness of the walls. Let's add it and get 33 cm. This is an approximate calculation of a subwoofer housing with a bass reflex for a specific speaker. Please note that this article is only a general guide; it does not take into account many of the subtleties and nuances that arise during the work process.

LOVE STATISTICS

In October 2004, we for the first time began to measure the frequency response by sound pressure in the interior of cars included in the “Systems” section. Measurement data has been and continues to be accumulated in the form of files in the format of the Phonic PAA2 analyzer, which, among other things, has the ability to average the measured characteristics. And so we decided to see what the frequency response would look like, which is a synthesis of the activities of professional installers over a year and a half. The voice of the people is the voice of God; during averaging, numerous individual characteristics and/or flaws should have been smoothed out as statistical noise, and general trends should have appeared. So here it is: for the first time, the frequency response is published, obtained on the basis of approximately 80 frequency characteristics taken over a year and a half.

The result of averaging the frequency response in the cabin for approximately 80 professional audio systems, paid for and accepted by customers. Individual characteristics were leveled out, and it became clear: people want to see approximately this frequency response in their car. But you won’t go against the people, and there’s no point in doing so

It turned out to be a curious picture, a reason to think about the morals prevailing in society. But we will now focus on the low frequency region. General trend: people want to have sound pressure at low frequencies significantly higher than at mid frequencies. If they didn’t want to, they wouldn’t have had such frequency response done. Using other functions of PAA2, we even isolated the deviation of the frequency response at low frequencies from the horizontal straight line. At a frequency of 40 Hz, the increase in the “folk” frequency response was more than 14 dB. What does this mean? Let's assume that you have such magical midbass that they are capable of providing a smooth frequency response up to 40 Hz. And now the power supplied to them is only, say, 5 W. To achieve such a boost in bass, at 40 Hz the power supplied to the speakers must be approximately 25 times greater. Not 5 W, but 120 - 130. Really? No, of course, with normal 6-inch speakers the thermally permissible power is even lower, and long before that the distortion will exceed all conceivable limits. That is why this part of the frequency spectrum in a car is played by a specialized speaker, for which a hundred watts is not a disaster, but normal operation.

In order to focus in this conversation on low frequencies, we have isolated the low-frequency region from the graph of the “national” frequency response in the form of a deviation of the frequency response from the horizontal. It’s hard not to notice that below 80 Hz the tastes of car audio lovers crystallized into a dome-shaped frequency response with a maximum at 40 Hz

By the way, we couldn’t resist and performed the same operation, leaving in the sample only the cars that took high places in car audio competitions. As expected, the “average champion” frequency response looks much more modest than the “national” one.

The approach to bass topics of super-professionals - winners of high-ranking car audio competitions - is more restrained. In everyday life, the sound of the bass of many competitive cars is considered a bit dry, but it is precisely this that is most correct and reliable

By leaving in the sample only those systems in which the subwoofer was designed according to the principle of a closed box, and not a bass reflex, we confirmed what we already knew: it is the WY that gives the most even frequency response. With the right choice of parameters, of course

Those familiar with past issues of “V.V.” We should have noticed signs of some deceit in the above logic. Indeed, there is a transfer function of the interior, thanks to which it is in the car (that is, where the masses demand it) that the frequency response, starting from a certain frequency, rises by itself, without any human intervention. It’s good that you really noticed the transfer function of the cabin - a true blessing from God for car audio enthusiasts; without it, it would have been incredibly difficult to obtain the desired characteristic even with the help of a subwoofer, and at high volume levels (let’s not forget about this taste feature) - and completely impossible. However, the fact of the presence and uninterrupted operation of the transfer function does not eliminate the need for a separate bass section, but simply imposes certain requirements on its design and calculation. Or do we need to remind you about the transfer function? Now is the time, there’s no way to continue without her.

Making your own port

The bass reflex, just like the speaker, is involved in sound reproduction. To avoid the interference effect, the channel is placed closer to the low-frequency emitter at a distance not exceeding its wavelength. Rigid structures are used as FI, for example, plastic sewer pipes are used in homemade products.

But when trying to calculate a bass reflex for a subwoofer, consumers are faced with the fact that the diameter of such pipes does not coincide with the calculated values, so the pipe is made from a dense material at hand - whatman paper. In order to make a channel yourself, you will need:

newsprint;
whatman;
glue.

A strip cut from whatman paper, the width of which coincides with the length of the tube, is wound in several turns on the surface of newsprint. In this case, epoxy glue is applied before each turn. It is obtained by mixing resin and hardener according to the instructions. After all the turns have been completed, the product is wrapped in a circle with thread to impart rigidity and placed to dry.

After a day, the base is removed. If difficulties arise, it can be broken from the inside and taken out in parts. A manufactured channel of this type has good strength and is easily subject to additional processing. Next, the resulting tube is installed in the hole of the speaker, but not all the way, and listening to the sound begins. In the factory, a special device is used. Such a device operates on the basis of a multivibrator, which is tuned to the resonant frequency of the dynamic head. After connecting the speaker, the generator starts and the length of the pipe is adjusted to the maximum fluctuation of air in it.

You can do the same setup yourself. To do this, a low frequency signal is supplied to the input. The tube is moved forward or immersed inside the box, and then the volume of escaping air is assessed. Having established the position of its maximum outlet, the excess pipe is removed from the outside, and the port itself is sealed. If desired, to give the structure a finished look, open the pipes, but you can do without it.

MECHANISM OF GOD'S GRACE

We decided to remember everything, so let’s do everything. So, it was predicted, observed, explained theoretically and strictly confirmed by practice: if a speaker with a flat horizontal frequency response is working in the car interior, then when the signal frequency decreases, starting from a certain value, the sound pressure in the cabin will increase, while the power supplied to the speaker remains unchanged. The frequency at which this occurs is determined by the size of the cabin.

This is where some people get confused: the compression effect, also known as the effect of the transfer function, is sometimes confused with the resonances that occur in the cabin. For clarity, let's do a mental experiment. Let there be acoustics installed in the car interior, to which we send a sliding tone signal. Starting from the top. While the signal frequency is high, the sound waves are short, they run merrily, at the speed of sound, around the cabin, being reflected and absorbed at its boundaries. When the wavelength, increasing with decreasing frequency, begins to be comparable to the smallest (!) size of the cabin, this is usually its height, a standing wave will arise, and depending on where the listener is located, it can hit the point of minimum or, conversely, maximum intensity of sound vibrations. It is important that there are several such frequency values (unless the salon is shaped like a ball with the listener strictly in the center), and the effect perceived by the listener (or the microphone, if measurements are being taken) significantly depends on their coordinates in the salon.

We are moving lower in frequency. At some point, the wavelength will become so large that even half of its length will no longer fit along the largest(!) dimension of the cabin (this, of course, is usually its length). From this moment on, the rise in frequency response will begin completely free of charge and with impunity.

What exactly happened at this magical frequency, why did it happen and how will events unfold next? Let's figure it out one last time so we can consider the issue closed. To do this (mentally again, doesn’t this tire you?) in Suvorov style, let’s take the magic frequency in pincers from two directions.

We start the attack from above. An ideal speaker is designed in such a way that if constant power is supplied to it, then at any frequency above the frequency of its main resonance and up to the upper frequency limit, which we will not talk about now, because the topic is different, the sound pressure it creates will be constant. This is an ideal, of course, in the real frequency response of acoustics we see that different details appear here and there, but the general course of the frequency response is exactly like this if you close your eyes to the little things. But now you will have to take my word for it (to avoid formulas, even if they are not very fluffy).

The sound pressure created by a speaker in an infinite space is proportional to the oscillatory acceleration of the cone. In order for this acceleration to remain constant as the frequency decreases, the oscillatory speed must increase inversely proportional to the frequency (twice as the frequency decreases for each octave), and the amplitude of the diffuser oscillations must increase inversely as the square of the frequency (that is, quadruple with each octave as you move down the scale frequency

This is how it really happens, which (even if not quantitatively) can be seen with the completely naked eye. Let's apply a sinusoidal signal to the speaker, say 100 Hz, raising the level to such a value that it is clearly audible. We'll see: the diffuser vibrates with a double amplitude of about two millimeters. Without changing anything, let's raise the frequency to 200 Hz. It is audible, to put it mildly, no worse, but vibrations of the diffuser are no longer easy to notice; the amplitude is now half a millimeter. Let's raise the frequency to 1000 Hz. The speaker screams like a victim, and even a hawk's eye cannot see the movement of the diffuser; their scope has dropped to two hundredths of a millimeter. So, remember: in limitless space, in free air, the sound pressure created by the speaker will be constant if the amplitude of the diffuser oscillations increases fourfold for each octave of frequency reduction. And only in this case.

Now let's go from the other end of the frequency scale, from below. Imagine that a speaker is attached to the outside of a box, which in this experiment will represent the interior of a car (so as not to spoil an expensive vehicle), and the diffuser oscillates at a very low frequency, for example, 1 Hz. Or 5. Or 10. There is no need to talk about any propagation of sound waves inside a box, even if it is the size of a car, the length of a sound wave with a frequency of 10 Hz is more than 30 m, and at a frequency of 1 Hz - even 340. This means that with When the diffuser oscillates, pressure fluctuations in the cabin box do not occur through the propagation of waves, but everywhere at once, just as if the speaker were a piston and the inside of the box was a cylinder. Now answer: how will the change in pressure in the box depend on the amplitude of the diffuser oscillations? Of course, linearly, for every millimeter of movement of the piston-diffuser, the volume inside the box will change by the same amount, a pump, in a word.

Let's compare the results of thought experiments (fortunately) at high and extremely low frequencies. When we walk from above, the sound pressure in the cabin spreads along a wave mechanism, the cabin is large, the waves are small, for them it can be considered an endless expanse. The speaker conscientiously tries to create the same sound pressure at any frequency, and to do this, with each octave, moving down, the amplitude of the diffuser’s vibrations increases fourfold.

At low frequencies, the speaker tries to do the same thing: as the frequency increases by an octave, the amplitude of the diffuser's oscillations decreases fourfold. But here, as we just agreed, the pressure fluctuations in the cabin (and this is the sound pressure) are proportional to the first power of the diffuser oscillation amplitude, which means they obediently drop fourfold with each octave increase in frequency. Or it grows (again fourfold) when moving in the opposite direction.

What is a change in sound pressure of four times an octave? This is 12 dB in sound pressure, which is where this famous value actually comes from.

Somewhere these two curves (or rather, straight lines for now) must meet. This will happen near that same magic frequency, determined by the largest size of the cabin.

Of course, everyone understands: in nature, it doesn’t happen that you reach a certain frequency and, as if on command, everything becomes different. Here, so far down from the characteristic frequency, the compression mechanism works when the sound pressure is proportional to the stroke of the diffuser. Much above this frequency, a wave mechanism operates when the sound pressure is proportional to the square of the diffuser stroke. Around the frequency we are talking about, one mechanism gradually gives way to another. Gradually, and during this process, others occur in the cabin, so to speak, “cold waves splash, beat on the seashore.” Therefore, even the frequently seen pictures in which the horizontal section of the frequency response of the cabin, smoothly bending, turns into an inclined one is also a simplified vision of the picture, our repeated measurements show: in the transition region (in practice 75 - 100 Hz) cabin acoustics are extremely unpredictable, and we will have to act within the framework of one idealization or another. Up to the extreme, but visual.

But before moving from some completely sinless speaker to one more similar to the real one, let’s determine the frequency at which the wave mechanism of sound propagation in the cabin gives way to compression. Or - at which the rise in frequency response so desired by us begins without any effort on our part.

Physically, this frequency corresponds to the moment when half of the longest wave that appears in the cabin will no longer fit in this cabin, be it across, or along, or placed on its butt. In reality it is always along, the cars are still longer than in other directions. When half a wave ceases to fit, this means that at all points in the cabin the pressure of the medium (air or its mixture with tobacco smoke) at any moment of time changes in one direction: it either increases everywhere, or decreases everywhere in the next half-cycle.

Hence the simple and popular rule: take the number 170 (half the speed of sound in meters per second) and divide it by the largest cabin size. This is where a big and hot bazaar usually begins about what transfer function each car has, based on its size. Different, of course, who can argue. But if we take into account all the factors that influence this function, we will see that the actual size of the car is the most noticeable, but far from the most important.

Let's be realistic and finally stop needlessly mentioning the Oka and Stretch based on the Lincoln Town Car. The few people who want to engage in high-quality scoring of one and the other will certainly find solutions as non-standard as their cars. In real life, the dimensions of the interior do not vary as much as the dimensions of the car, and the dimensions of most cars do not differ by an order of magnitude.

I bet: with a 95% probability, the length of your car is from 4 to 5 m. With a 90% probability, it is from 4.1 to 4.6. The salon will have from 2.2 to, say, 2.5 m. The frequency of the start of the rise in the frequency response, respectively, is 75 ± 5 Hz. Is it necessary to break spears about this? The range in choosing subwoofer parameters, as long-term observations show, is much wider, and the influence of the wave mess that occurs in the cabin near this frequency is much stronger. It's better to focus on the basic principles, the details will come in due time. After all, until now we have based our theories on the idea that the speaker is ideal and reproduces any frequencies. But this does not happen even in the driest theory.

An extremely, fantastically idealized picture of what is happening in the salon. The fantastic thing is that we assumed: the subwoofer has a resonant frequency that is almost zero, and it maintains the generated sound pressure unchanged down to the lowest infrasound frequencies. This is fantasy, but it is still needed. And the idealization is that the smooth transition from the horizontal frequency response to the inclined one (both for the subwoofer and for the transfer function) is conditionally replaced by a sharp break. So far this will not significantly affect the logic. The frequency at which the inclined branch of the frequency response of the transfer function begins is taken to be 80 Hz, which is not far from the real values.

The diffuser stroke as a function of frequency is plotted on a logarithmic scale, so the fact that it increases by a factor of 100 when the signal frequency decreases by a factor of 10 is expressed by the slope of the straight line.

If we assume that such a subwoofer really exists, the frequency response in the cabin, in an ideal case, would steadily strive upward with a slope of 12 dB/oct., while the amplitude of oscillations of the diffuser, very modest even at a fairly low 100 Hz, would try to reach the lowest frequencies completely insane values. In real conditions, below 20 Hz, the car body begins to “breathe” so much that the sound pressure stops increasing, but the subwoofer does not know this and continues to pound like crazy. If this is not prevented

Third step: adjust output sensitivity

The output sensitivity adjustment filter also looks like a wheel for scrolling with a screwdriver and is designated “GAIN” or “LEVEL”.

There is a misconception that this parameter is responsible for the volume of the subwoofer, in fact this is not the case, even though when set to the upper positions the volume does increase. This filter is responsible for the coordinated operation of the head unit and subwoofer, and is configured using a specific method that has four simple steps:

set the controls on the radio and amplifier to minimum and the sound signal will sound to check;
the volume gradually increases until the first distortions in the sound appear, after which it returns to the last position at which there was a clear sound;
then the regulator on the amplifier rotates upward until the first sound distortions appear;
as soon as distortions appear, the regulator returns to the extreme position at which they did not exist.

THERE IS ANOTHER FREQUENCY

A speaker in a “closed box” design, which also includes the case of an acoustic screen, is like an infinitely large closed box, has a strictly defined lower frequency limit of effective radiation. This is the fundamental resonance frequency of the speaker in the box. Below this frequency, with the input power still constant, the sound pressure drops at a rate of 12 dB/oct. And the amplitude of the diffuser oscillations stops growing. Below the resonant frequency it remains constant. In home acoustics, this is what is considered the lower frequency limit; below that, the speaker produces very little sound. And this is exactly what the inventor of the closed box, Edgar Vilchur (last issue of V.V.), had in mind when he spoke of the “optimal resonant frequency.” Optimal is when the amplitude does not go beyond linearity. A 6-inch speaker with a resonant frequency (in a box) of 20 Hz at lower frequencies will choke due to the excessive movement of the cone. And if the resonant frequency is not 20, but 60 Hz, the increase in amplitude at this frequency will stop (being 9 times less than it would be at 20 Hz at the same sound pressure) and the distortion will remain normal.

But this is at home, there is space, but in our cabin there is cramped space and a transfer function. With the steepness of the slope, let me tell you, the same 12 dB/oct. This means that at home it turns out like this: as soon as the resonant frequency is passed, the amplitude of the diffuser’s oscillations stops growing, therefore, as the signal frequency decreases, the sound pressure will fall in inverse proportion to the square of the frequency (this is exactly 12 dB/oct.). And in our salon, if the amplitude of the diffuser oscillations remains constant where the compression zone has already begun, this means: an “acoustic pump” operates with a constant piston stroke and creates a constant sound pressure independent of frequency, that is, a horizontal frequency response. Or, if you prefer, in a different way. Sound pressure drops at a rate of 12 dB/oct., and the transfer function grows at the same pace. And so it turns out that way. But where it will start to fall and where it will grow is a separate question.

A slightly more realistic, but still suboptimal case. With the best intentions, a subwoofer with a resonant frequency of 20 Hz was designed for the car. A home audiophile's dream. What happened: up to 20 Hz, the frequency response in the cabin grows under the influence of the transfer function, and only there it turns into a horizontal line (which a home audiophile cannot even dream of). Neither ordinary people, nor even more famous champions want such an frequency response, as can be seen from our statistics. Including because the diffuser stroke at ultra-low frequencies that are not very necessary for sound is still very large.

In real life, this happens when, out of foolishness or mischief, a subwoofer head with a low resonant frequency, intended for installation in a box, is mounted in the rear shelf and it operates in infinite screen mode (free air)

Closed box

This type of design is the simplest. A closed box for a subwoofer is easy to calculate and assemble. Its design is a box of several walls, most often 6.

Advantages of ZY:

Simple calculation;
Easy assembly;
Small displacement of the finished box, and therefore compact;
Good impulsive characteristics;
Fast and clear bass. Plays club tracks well.

A closed box has only one drawback, but sometimes it is decisive. This type of design has a very low level of efficiency compared to other boxes. A closed box is not suitable for those who want high sound pressure.

However, it is suitable for fans of rock, club music, jazz and the like. If a person wants bass, but needs space in the trunk, then a closed box is an ideal option. A closed box will not play well if the wrong volume is selected. What volume of box is needed for this type of design was long ago decided by experienced people in car audio through calculations and experiments. The choice of volume will depend on the size of the subwoofer speaker.

The most common speaker sizes are: 6, 8, 10, 12, 15, 18 inches. But you can also find speakers of other sizes; as a rule, they are used very rarely in installations. Subwoofers with a diameter of 6 inches are produced by several companies and are also rarely found in installations. Mostly people choose speakers with a diameter of 8-18 inches. Some people indicate the diameter of the subwoofer speaker in centimeters, which is not entirely correct. In professional car audio, it is customary to express dimensions in inches.

Recommended volume for a closed box subwoofer:

an 8-inch subwoofer (20 cm) requires 8-12 liters of net volume,
for 10-inch (25 cm) 13-23 liters of net volume,
for 12-inch (30 cm) 24-37 liters of net volume,
for 15-inch (38 cm) 38-57 liters net volume
and for 18 inches (46 cm) you will need 58-80 liters.

The volume is given approximately, since for each speaker you need to select a certain volume based on its characteristics. The setting of a closed box will depend on its volume. The larger the volume of the box, the lower the tuning frequency of the box will be, the bass will be softer. The smaller the volume of the box, the higher the frequency of the box, and the bass will be clearer and faster. You should not increase or decrease the volume too much, as this is fraught with consequences. When calculating the box, adhere to the volume that was indicated above. If there is too much volume, the bass will turn out vague and indistinct. If the volume is not enough, then the bass will be very fast and “pound” the ears in the worst sense of the word.

A lot depends on how the box is configured, but an equally important point is “Setting up the radio.”

COLLISION OF TWO FREQUENCIES

This is where we come to the main secret of car subwoofers. And it lies in the fact that they begin to work where home acoustics finish their work. The frequency of the front-subwoofer section is 50 - 100 Hz. These are extreme limits; most systems are tuned to cut at a frequency of no lower than 60 and no higher than 85 Hz. It is inside this corridor that the magic frequency of the beginning of the rise in the frequency response under the influence of the transfer function sits. And the resonant frequency of the subwoofer should be approximately there (in the box), if the system designer is faced with the task of obtaining a sane frequency response.

The illustrations below, extremely idealized for clarity, show typical cases of interaction between the resonant frequency of a subwoofer and the transition frequency of the transfer function.

A kind of paradox: in the practice of home acoustics, in order to obtain a lower limit frequency of 50 Hz, it is necessary to make the resonant frequency of the bass speakers in the design approximately the same, but in a car, in order to smoothly and calmly reach 20 Hz, the resonant frequency of the lowest frequency link in the system you can select in the region of 60 - 80 Hz. In this case, at home there will be a “woofer”, and in the car there will really be a SUBwoofer, according to the final result.

In principle, this is the main thing on which the calculation of a subwoofer in the design of the ZYA type is based, it’s just a small matter: learn to choose a subwoofer and the volume of the box, which, taken together, will allow you to “get into” the setup. We'll choose in exactly one month.

Champion selection. If the resonant frequency of the subwoofer (taking into account the design, assembly) is close to the “magic frequency” on the transition function, this, under certain conditions, can produce a perfectly flat frequency response, and the diffuser stroke does not increase below 80 Hz, maintaining completely acceptable values. At the same time, let us pay attention once again: a SUBwoofer, capable of sounding up to 20 Hz with constant output, has a natural resonant frequency of about 80 Hz. So this is what is happening here. Now, if you choose a resonant frequency below the transition region, without, of course, reaching the fanaticism from the previous example, the frequency response below 80 Hz will rise parallel to itself, approaching the “national” one, but without a pronounced hump at 40 - 50 Hz, the origin of which is has nothing to do with a closed box

Another example of poor choice of subwoofer parameters. Either by taking an unsuitable speaker (intended for free air), or by being too greedy with the volume of the box, they made a subwoofer with a resonant frequency noticeably higher than the “magic” one. Result: the output of the subwoofer begins to fall where the transfer function is not yet working at full strength, and when it finally gets down to business, it will be too late, the frequency response will fail, and this will have to be compensated by increasing the power supplied to the subwoofer (which it may not like) and correction Frequency response in the area of separation between the front and the subwoofer, this could also be somewhere here, at 80 - 100 Hz