Closed speaker systems have become very widespread in recent years, which until recently were the only type of speakers for high-quality playback both in our country and abroad. And only in recent years, speakers with a bass reflex (AS with FI) and speakers with a passive radiator (AS with PI) have broken the monopoly of closed speakers.
Nevertheless, the acoustic design of a closed box is currently one of the most common designs of high-quality speakers in Western Europe and is quite widely produced in the USA, as can be seen from the table (data from 1984):
| A country | Closed systems, % | Speakers with bass reflex, % | Speakers with passive radiator, % | Other systems, % |
| USA | 42,7 | 32,4 | 8,6 | 16,3 |
| Western European countries | 60,8 | 31,7 | 6,5 | 1,0 |
| Japan | 27,9 | 62,3 | 9,8 | — |
In Fig. Figure 1 shows a typical closed speaker.
Tannoy TS2.8 active subwoofer in closed box acoustic design.
The advantage of a closed speaker is that the rear surface of the driver cone does not radiate and thus there is no “acoustic short circuit” at all.
The disadvantage of closed speakers is that the diffusers of their heads are loaded with additional elasticity of the air volume inside the design. The presence of additional elasticity leads to an increase in the resonant frequency of the moving system of the head in a closed design ω01 and, as a consequence, to a narrowing from below of the reproduced frequency range. The value of the additional elasticity of the air volume SВ can be found as:
SB=γp0S2eff/V, (1)
where γ is the adiabatic exponent, Seff is the effective area of the head diffuser, V is the internal volume of the design body.
The effective area of a diffuser is considered to be 50–60% of its structural area. For a round diffuser with a diameter d Seff=0.55S=0.44d2. This is equivalent to the effective diameter of the diffuser being 0.8 times the design diameter. The elasticity SВ is summed up with the self-elasticity of the suspension of the movable system of the head S0 and as a result the resonant frequency of the head in a closed design is calculated by the formula:
ω01=√((S0+SB)/m)=ω0√(1+SB/S0), (2)
where m is the mass of the movable system of the head.
As can be seen from formula 1, the elasticity of the air volume inside the design is inversely proportional to this volume. The elasticity of a moving system can also be expressed through the elasticity of a certain equivalent volume of air VE having elasticity S0. Hence the resonant frequency of the head in a closed design:
ω01=ω0√(1+VE/V) (3)
To ensure that the resonant frequency is not excessively high, heads with a heavier moving system are sometimes used, which makes it possible to slightly reduce the resonant frequency of the head in a closed design, as can be seen from formula 2. However, it should be borne in mind that increasing the mass of the moving system reduces the sensitivity acoustic system, as can be seen from the formula for standard sound pressure:
where A is a frequency-independent multiplier, Rr is the output resistance of the amplifier (oscillator), Rk is the active resistance of the voice coil, and is the effective radius of the head.
The so-called small-sized acoustic systems (MAC) have especially low efficiency, in which the elasticity of the volume inside the design is significantly greater than the elasticity of the fastening of the moving head system.
Such systems, in which the elasticity of the moving system is determined by the elasticity of the air volume inside the design, are called systems “with a compression suspension” of the head.
The standard sound pressure pst of such a system at frequencies ω>ω01, where pst is frequency-independent, is determined as follows:
rst=2.65*10-3√(f301V/Q01), (5)
where Q01 is the quality factor of the head in a closed design (measurement methods can be found in the article “Measuring Thiel-Small parameters at home”).
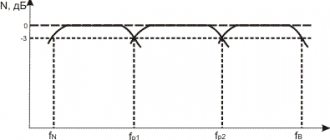
As follows from formula (4), the unevenness of the frequency response of closed acoustic systems in the low frequency region, just like open ones, is determined by the quality factor (Fig. 2).
Rice. 2. Frequency response of a closed system (AFC)
When Q01<0.707, the frequency response of the speaker decreases uniformly with decreasing frequency into the low-frequency region, and the unevenness manifests itself as a decrease at the resonant frequency ω01 compared to higher frequencies. At 0.70701<1, the frequency response has a small peak at frequency ω1 and then a decline at the resonant frequency ω01. The unevenness of the frequency response is determined by the rise at the peak ω1, and the decline at the resonant frequency ω01. When Q01>1, the unevenness of the frequency response is determined only by the face at frequency ω1 relative to the horizontal part of the response.
The unevenness of the frequency response depending on the quality factor of a closed speaker is shown in Fig. 3.
Rice. 3. Dependence of the unevenness of the frequency response of a closed acoustic system on Q01.
As follows from the figure, the minimum unevenness in the frequency response of closed speakers occurs at quality factor Q01=1 and is 1.3 dB. The desired quality factor of the head itself is determined from the condition:
Q=Q01/√(1+Veff/V) (6)
Studies have shown that the quality factor of heads intended for closed speakers should not exceed 0.8–1.
Otherwise, the head turns out to be “dedamped”. This means that when it is excited, i.e. when a music or speech program voltage is applied to it, the head, in addition to oscillating in time with the applied voltage, will also oscillate with a natural frequency close to the resonant frequency.
For listeners, this will manifest itself in the fact that the sound of this frequency will be mixed into the sound of the program as a kind of “hum”, “impurity” of low tones. Note also that if the head is placed in a closed box, the uniformity of the frequency response in the mid and high frequencies deteriorates due to resonant phenomena in the design.
To eliminate them, the internal surfaces (especially the back wall) are covered with sound-absorbing material and part of the volume is filled with it. In addition, by filling the internal volume with loose sound-absorbing material, another goal is pursued - to change the thermodynamic process of compression-expansion of air in the design.
Without filling, the process of compression and expansion of air inside the design is adiabatic. By filling the design with loose sound-absorbing material, you can change the adiabatic process to an isothermal one.
In this case, the internal volume of the design seems to increase by 1.4 times, since the coefficient γ in formula (1), which is 1.4 for the adiabatic, is replaced by a value equal to one for the isotherm. Accordingly, the resonant frequency of a closed speaker decreases.
This reduction in the limit (for a compression speaker) reaches √1.4, since for it the elasticity of the head suspension can be neglected. Otherwise, the resonant frequency of the head ω01' can be found as:
ω01'= ω01√((1+0.75 *S/S0) ∙ (1+S/S0)), (7)
Examples of calculating a closed box
Example No. 1 . Let, for example, use a speaker with parameters f0=30 Hz, Q=0.4, Ve=60 l. We find the preliminary A = 2.65*10-3√(303*100*10-3/0.4)=0.218.
Let it be necessary to select a design volume V for this speaker, at which the drop in frequency response should be 6 dB at the cutoff frequency of the speaker fgr = 40 Hz.
According to Figure 6, from the point ωrp/ω0 = 40*30=1.33 on the horizontal axis, we restore the ordinate to the intersection with the curve marked 6 dB and from this point we draw a straight line parallel to the abscissa axis to the intersection with the V/Ve curve. We get V/Vе = 0.95. From here V = 0.95 Vе= 0.95*100=95 l. This value of V/Ve along the right vertical axis has the value √(1+V/Ve)=1.4. Therefore, pst = 2.18 * 1.4 = 0.305 Pa. According to the graph in Figure 5, we find the ratio ωrp/ω0=f01/f0=1.4. Hence f01 = 1.4f0=1.4*30=42 Hz.
Example No. 2 . You can calculate a closed box not only using graphs, but also using the given formulas. Let, for example, you need to calculate the volume of a closed box of speakers with a lower limit frequency of 50 Hz, having a 10GD-36 head (f0 = 38 Hz, Q = 0.8, Ve = 60 l).
- We determine the volume of decoration from formula (3): V = 60/(50/38)2-1) = 83 l.
- Find the quality factor of the speaker in a closed box from formula (6): Q01=0.8√(1+60/83) = 1.05
- In accordance with Fig. 3, the minimum unevenness of the frequency response occurs at Q0=1. So the resulting unevenness in the frequency response due to the peak at frequency ω1 is practically minimal and amounts to only about 1.5 dB.
Acoustic design with passive radiator (PI). Calculation and setup
There is another type of acoustic design of a loudspeaker that can ensure that the loudspeaker reproduces low frequencies with relatively small dimensions of the box. It has several names, of which the most correct are: bass reflex with a passive radiator or FI with a closed hole. This design is also called a passive radiator (PI) or passive radiator.
The peculiarity of this bass reflex is that the loudspeaker is placed in a box that has a hole near its installation site, with a movable system of a second loudspeaker fixed in it without a magnetic system and a centering washer. The diameter of the passive radiator cone is approximately equal to the diameter of the loudspeaker cone. The hole in the voice coil is sealed and in this place an additional weight is attached to the diffuser. The weight of the load depends mainly on the volume of the box and the resonant frequency of the bass reflex.
The principle of operation with a passive radiator is similar to the principle of operation of a conventional bass reflex. At the resonant frequency of a closed FI, the diffuser of the passive radiator oscillates in phase with the diffuser of the main loudspeaker, ensuring effective signal reproduction in the low-frequency region. Thus, unlike the main bass reflex, here the mass in the hole is replaced by the mass of the movable passive radiator system, including an additional weight.
The weight allows you to more simply than is done when measuring the size (volume) of the passage in a conventional bass reflex, to regulate the resonant frequency of the bass reflex. When reducing the volume of the box of a conventional bass reflex, it is necessary to increase the volume of the passage or reduce the area of the hole, which reduces the efficiency of the bass reflex. A bass reflex with a closed hole is free from this drawback and this is its main advantage.
Passive radiators found application in acoustic systems of the USSR era, such as: “25 AS-128 Electronics” and “35 AS-015 Electronics” . In modern speakers, this design is used in PMC IB2i or the Sunfire True Subwoofer . A passive radiator can be of almost any shape, round, square or oval, for example, as shown in the photo below:
Another positive quality of a bass reflex with a closed hole is a slightly greater in-phase movement of both diffusers in the resonance region compared to the movement of the air volume in the hole and the speaker cone in a conventional bass reflex. The resonant frequency of a bass reflex with a closed hole is equal (as well as a conventional one):
fф = 1 : (2Π · (√mф · Сф)), where
- mf – mass of the moving system of a passive radiator plus the mass of air oscillating with it, attached to the diffuser, g;
- Sf is the resulting flexibility (the reciprocal of elasticity) of the volume of air in the box and the additional moving system, see dyn.
The calculation of a bass reflex with a closed hole is carried out as follows: by choosing the volume of the box Vf and knowing the effective diameter of the diffuser of the passive radiator Deff , determine the flexibility of the air volume from the expression:
Here the volume of the box Vf is expressed in cm3, and the effective diameter of the diffuser of the passive radiator Deff is in cm. Let us recall that the effective diameter of the diffuser is equal to:
Deff =0.85-0.9 Ddiff , where
- Ddif – the full diameter of the diffuser (the correct diameter to measure is from the center of the suspension (corrugation) on one side to the center of the suspension on the other side).
The equivalent effective diameter of an elliptical (oval) diffuser is:
Deq.eff = (0.85 – 0.9) · (√Db · Dm), where
- Db – large diameter of the ellipse;
- Dm – small diameter of the ellipse.
Since the flexibility of the diffuser suspension of the passive radiator Spod is much greater than the flexibility of the air volume of the box Sf , its influence on the total flexibility is extremely small and can be neglected. Overall flexibility is determined by the formula:
Ctotal = (Spod · Sf) · (Spod + Sf)
And when:
Spod >> Cf, Commun ≈ Cf.
Taking, as usual, the resonant frequency of a closed phase inverter equal to the main resonant frequency of the loudspeaker, find the mass mf corresponding to this frequency and the flexibility of the selected volume:
mf = 1 : (4Π2 ff2 Sf)
As mentioned above, this mass includes the mass of the passive radiator diffuser mrad and the added mass of air oscillating with it Δm , i.e.:
mf = mrad + Δm.
The value of Δm depends on the effective diameter of the diffuser and is determined by the expression:
Δm = (8 10-4) Deff3, g
Thus, the radiator diffuser must have the following mass:
mrad = mf – Δm;
In practice, this value will be equal to the mass of the load that needs to be installed on the diffuser. To facilitate the necessary calculations, the table shows the values of volume flexibility Cf for boxes with a volume of 20 to 80 liters and passive radiator diffusers with an effective diameter of 15 to 22 cm, and also indicates the value of the attached air mass Δm for the same diffuser diameters.
| VФ, l | Flexibility of box volume, cm/din 10-6 at Def, cm | ||||||
| 15 | 16 | 17 | 18 | 19 | 20 | 22 | |
| Δm, g | 1,7 | 3,3 | 3,9 | 4,7 | 5,5 | 6,4 | 8,6 |
| 20 | 0,45 | 0,35 | 0,27 | 0,22 | 0,17 | 0,14 | 0,1 |
| 30 | 0,67 | 0,52 | 0,41 | 0,32 | 0,26 | 0,21 | 0,15 |
| 40 | 0,9 | 0,69 | 0,55 | 0,43 | 0,35 | 0,29 | 0,19 |
| 50 | 1,12 | 0,87 | 0,68 | 0,54 | 0,44 | 0,36 | 0,24 |
| 60 | 1,35 | 1,04 | 0,82 | 0,65 | 0,52 | 0,43 | 0,29 |
| 70 | 1,57 | 1,21 | 0,95 | 0,76 | 0,61 | 0,5 | 0,34 |
| 80 | 1,8 | 1,4 | 1,09 | 0,87 | 0,7 | 0,57 | 0,39 |
The flexibility value of the air volume in boxes with intermediate values and the effective diameter of the radiator diffuser is determined by interpolation using two adjacent flexibility values, between which the accepted dimensions are located.
As an example, let’s determine the mass of the load that must be mounted on a passive radiator diffuser with a diameter of Ddif = 22 cm, installed in a box FI with a volume of Vph = 50 l at a resonant frequency of FI of 45 Hz. Effective diameter:
Deff = 0.87 → Ddiff = 0.87 · 22 = 19 cm.
Using the table, we find the flexibility of the air volume in the box with such an effective diffuser diameter: this flexibility is equal to:
Sf = 0.44 10-6 cm/din.
The total mass of the diffuser should be:
mf = 1: (4Π2 ff2 Sf) = 106: (4Π2 452 0.44) ≈ 28.4 g
The added mass of air, according to the table, is equal to Δm = 5.5 g. Therefore, to obtain a given resonant frequency, it is necessary to install an additional weight:
mrad = mf – Δm = 28.4 – 5.5 ≈ 23 g
The additional load is a steel or copper (brass) disk with thickness h , which for steel, depending on the diameter of the disk d , is equal to:
h = (0.16 mrad): d2
As stated above, the magnetic system and centering washer are removed from the speaker designed to function as a passive radiator. This is done in order to increase the flexibility and linearity of the movement of the moving system, and eliminate the danger of touching the voice coil. This does not reduce the effective volume of the box. An idea of the design of a passive radiator installed next to a loudspeaker is shown in the figure below, which shows how an additional weight in the form of a disk is attached to the center of the diffuser with a bolt and nuts. The hole in the diffuser is sealed with a piece of hard paper (whatman paper or thin cardboard) with teeth glued to the diffuser with celluloid or other glue, for example BF-2. It goes without saying that the fundamental resonant frequency of a loudspeaker designed for a passive radiator does not matter at all. Or you can buy ready-made passive radiators; they are now widely available.
When designing a bass reflex with a closed hole, you should not make it with a volume of less than 30-40 liters with a resonant frequency below 50 Hz, because an increase in the mass of the passive moving system, as well as the mass of air in the passage of a conventional FI, worsens the transient characteristics of the loudspeaker.
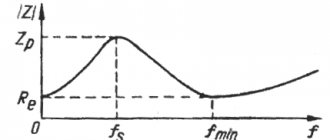
You can check the correct settings of the made phase inverter either by the amplitude of oscillations of the passive radiator visible during FM resonance, or by the volume that increases with resonance, which can be verified by placing a piece of plywood between the diffusers and bringing your ear to the diffuser of the passive radiator. Also, as in a conventional bass reflex, the frequency response of the loudspeaker impedance in a closed-hole bass reflex should have two maximums of almost the same height.
The box for the bass reflex can be made from plywood or chipboard 8-12 mm thick, but it should be noted that it should not have any cracks. It is useful to place sound-absorbing material inside the box, for example, 15-30 mm thick foam rubber, which will smooth out the frequency response of the speaker in the mid-frequency region.
Based on materials from the magazine “Radio”, 1974, No. 1
Nonlinear distortion
Nonlinear distortions of conventional electrodynamic heads are embedded in traditional designs of magnetic systems with an asymmetrical and uneven distribution of magnetic induction in the magnetic air gap [2] and an asymmetrical conical shape of diffusers that have a “parachute effect” of air resistance, as well as asymmetrical placement of voice coils in the magnetic system and nonlinear flexibility of suspensions of mobile systems [1].
Rice. 3. Cross-section of voice coil 1 in magnetic system 2 and graphs of magnetic induction.
In dual heads of the “diffuser to diffuser” type, the following effects are achieved:
- the nonlinearity of the flexibility of the suspensions of moving systems is partially compensated by:
- the resulting shape of the emitter becomes symmetrical;
- the asymmetrical arrangement of voice coils in magnetic systems is compensated; this is most fully achieved by selecting examples of heads with the same displacement of the voice coils, caused by an error in the assembly,
- the resulting displacement of the moving system in the piston range of the dual heads becomes symmetrical relative to the magnetic system due to the compensation of the force of attraction of the voice coil with current to the magnetic circuit and the unevenness of the magnetic induction in the gap of the magnetic system.
In Fig. Figure 3 shows the cross-section of the voice coil 1 in the magnetic system 2 and the graphs of the dependence of the magnetic induction B1 and B2 in the area of the gaps of the double heads BA1. BA2. The values of x and x2 correspond to the depth of the gap.
In dual heads of the “diffuser-by-diffuser” type, only the asymmetrical arrangement of voice coils in the air magnetic gaps is eliminated by selecting examples of heads with opposite displacement of the voice coils, as well as the unevenness of the frequency response in the low-frequency band [3].
Amplitude-frequency response (AFC)
The amplitude-frequency response (AFC) of the electrodynamic head is the dependence of sound pressure on the frequency of the reproduced signal at a constant power supplied to the voice coil.
All heads produced to date have uneven frequency responses [2], and the frequency responses of different copies of the same type of heads have different unevenness and slightly different frequencies of the main resonance of moving systems.
In dual heads, peaks and dips in the low-frequency band are partially compensated and the frequency response is smoother, but in the mid- and high-frequency bands these heads do not work as dual heads for the reasons stated above.
Equivalent volume of EDH
The equivalent volume of the electrodynamic head is the volume of air in the box, the flexibility of which is equal to the flexibility of the moving system of the head. In a double head, the suspensions work in parallel, so the resulting flexibility is half that of a single head. Accordingly, the equivalent volume of a double head is two times less than one and four times less than two single heads [7] (formula):
where Vosg is the equivalent volume of the dual head; Ve1. Ve2 - equivalent volumes of single heads.