↑ Hardware
The parts you need are 2 3.5 mm connectors for a sound card with shielded wires, a resistor of approximately 100 Ohms, a switch with one group of contacts (or an analogous button) of any kind, two crocodiles or clamps.
I was interested in digging around myself. ARTA writes that for accuracy it is desirable that Z be less than 100 ohms, much less than the input impedance of the sound card (supposedly it is about 20 kOhms). I think that a very low Z when measuring very large capacitances also worsens the accuracy, but in practice it is of little interest - a capacitance of 20,000 µF or 22,000 µF, it is more important to know that this capacitance is there, has not dried out, and if there is a need to select identical capacitances, then The absolute value is also not that important. I remind you once again - look at the result when the phase for capacitors is about -90, and for inductances +90. By the way, for capacitors with poor thermal dependence, you can see how Z changes due to the heat of the fingers.
You can check ancient containers from stocks (ESR is not visible, which is a pity), the drop in capacity due to drying out or breakage is immediately visible. There are no words, special devices are 1000 times better, but they cost money and take up space.
ARTA Software
Professional software for audio measurements and analysis of acoustic and electrical parameters of systems.
The program has received recognition due to its convenience and ease of use, and the ability to comprehensively analyze measurement data. The ARTA Software package consists of three modules: • ARTA – suitable for pulse measurement and is a powerful real-time signal analyzer. The construction of amplitude-frequency characteristics, phase-frequency characteristics, transient characteristics, group delay time, cumulative spectrum attenuation, dependence of pulse energy on time, decay graph, dependence of nonlinear distortions on frequency is carried out. • STEPS – allows you to measure the frequency response of the excitation signal in the form of a stepped sinusoid with a high dynamic range and high noise immunity. At the same time, harmonic distortion of 2, 3, 4, 5 and higher order is assessed. • LIMP – specializes in impedance measurements of low- and mid-frequency speakers and calculation of Thiel-Small parameters using the added mass and measuring box methods. The ARTA Software program adjusts the following values: amplifier output voltage, number of fragments per period of the test signal, sampling frequency, type of periodic noise signal, test signal level, cutoff frequency, measuring channel, number of measurements for the impulse response averaging method, and much more. For frequency response, group delay and phase response graphs there are options that allow you to change the degree of smoothing and use two time windows for construction. There is a calibration function for the measuring complex, as well as a one- and two-channel Fourier analyzer. Among the disadvantages is that the program cannot send measurement results to a printer or export them to a graphic format.
The program was developed by a scientist from Croatia, Ivo Mateljan. Since 1995, he has been the head of the Electroacoustic Laboratory at the Faculty of Electrical Engineering of the University of Split. From 2001 to 2006 he headed the Faculty of Electronics, and in 2006 he became a professor in the field of electrical engineering. In his free time, he is engaged in research work related to the study of the acoustic properties of materials, signal processing and virtual instruments.
ARTA Software is classified as a "shareware" program. The demo version can be downloaded from the official website. In this mode, the utility is fully functional except for loading and saving measurement results. However, through the clipboard, it is possible to import the received data into any free program for further processing. ARTA Software has two types of licenses: personal for 79 euros and commercial (multi-user) for 149 euros. The utility interface depends on the sound card and operating system used. After installation, configuration is required in accordance with the user manual.
The ARTA Software program, including the help system, is completely in English; there is no localization for this software.
To use the software, you must have a Pentium 600 MHz or higher class personal computer, a full-duplex sound card and a WDM or ASIO sound card driver for Windows. Required operating systems: Windows 2000, XP, Vista, 7. A complete list of supported sound cards is provided on the manufacturer's website. In Windows 7 and Vista, it is strongly recommended to use ASIO drivers. ARTA Software also runs on computers running Linux or Mac OS X using the Wine (for Linux) and CrossOver (for Mac) emulators.
Program distribution: shareware, from 79 euros
Official website of the ARTA Software program: https://www.artalabs.hr/
Discussion of the program on the forum
↑ Resistance measurements
At first I even wanted to omit this point - everyone has cheap digital Chinese testers, but after thinking about it, I found cases where this method could be useful. This is a measurement of low resistances - up to 0.1 Ohm inclusive. First you need to calibrate the device and short-circuit its probes. With a long cord I got 0.24 ohms. We will subtract this value from all measurements of low-resistance resistors. I have a handful of S5-16MV-5 resistors at 3.9 Ohms with an accuracy of 1%.
All resistors tested gave this result. 4.14 – 0.24 = 3.9 A handful of other low-resistance resistors were measured for verification, without any comments. The lowest resistance was 0.51 Ohm + - 5%. Measured value 0.5 ohm. Unfortunately, I could not find 0.1 Ohm in my supplies, but I am sure that there would be no problems with them either, you only need clamps with good contacts. In addition to measuring the resistance of low-impedance resistors, their inductance is of interest, especially for speaker filters. They are wire, wound in a coil. How significant is their inductance? I checked mainly low-resistance (up to 20 Ohms) resistors (high-resistance ones are not installed in acoustics and amplifiers) of types S5-16MV, S5-37V, S5-47V, PEVR-25, S5-35V. Their inductance was in the range of 2...6 microHenry. When measuring resistors of hundreds of ohms, their inductance was an order of magnitude higher.
↑ Inductance measurements
Let's move on to inductances. I don’t have precise inductances at the moment, so I just checked the qualitative, but not the quantitative, performance of the method.
These are measurements of the DM-0.1 inductor at 30 μH, it turned out plausible.
Here is the choke from the switching power supply. It also seems true. I can't vouch for the accuracy - there is room for research here.
↑ Capacitance measurements
The most interesting part is that there is something unclear, but the results are very interesting. Measuring range from 0.1 µF to 100,000 µF. Accuracy - several percent. More or less tolerable results are obtained from 0.01 µF, but measurements at low frequencies with a long cord with a large capacitance are impractical. I proceeded from the fact that capacitances of the order of fractions of a few microfarads for filters of acoustic systems and tone controls, and ULF coupling capacitors are of interest. There was hope to see ESR (it didn’t come true). Since I did not find precision containers at my place, I had to use the statistical method and common sense. At first I made and wanted to present a large table, but then the obvious truth came to me, for you only the results.
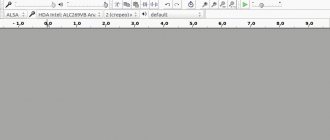
This is a 0.15 MKP X2 capacitor. At what frequency should I measure? Arta's coverage of this is vague. They say that it is necessary to measure at an impedance of less than 100 Ohms (one cell on the graph on the left is 800 Ohms) ... At 200 Hz it turns out 0.18 μF, at 20 kHz - 0.1 μF. From the basics of electrical engineering it is known that the current in a capacitance leads the voltage (-90 degrees), in inductance - on the contrary (+90 degrees), so we are guided by the gray curve and the phase shift number on the right. It is better if the shift is close to 90 degrees. Unfortunately, due to the limited frequency range, this does not always work out; in addition, often around 20 kHz the phase shift decreases, let’s not go into this area!
Here's an example. This is a 2.2 uF 15 V non-polar oxide capacitor. There is a strong suspicion of its poor quality and unsuitability for audiophiles. Non-electrolytic capacitors at higher voltages have a different phase diagram. Here the most reliable results are in the region of 0.5...1 kHz.
Capacitor 1 µF K10-47V for 50 V TKE N30. Reliable and stable results in the frequency range 1...20 kHz with a phase shift of 85...90 degrees. Curiosity drew me to see: what would happen if we measured oxide (electrolytic) capacitors? It turned out that it is possible to measure! The result is absolutely independent of the connection polarity; I even measured 4 banks of 10,000 uF connected in parallel and got a reliable result. I can judge the reliability because I have previously measured dozens of capacitors from 1 to 15,000 µF.
The result was 44 milliFarads. Pay attention to the phase characteristic in the region of several kHz; it takes on the character of inductance. Is this an imperfection of the instrument or is it really true that at such frequencies the capacitance of the plates works worse, and the inductance of the winding roll speaks louder and louder? Parallel connection of a small film container did not affect the graph. Due to the fact that loading graphics into the post is limited, I give a minimum of examples, so I’ll just repeat that you need to measure at the most “correct” phase (when you go through 0, you will get “inductance” from the capacitance and vice versa).
Sometimes it happens. This is one of the old soldered oxide containers. Clearly it belongs in a landfill. Can you imagine what such a container will do to the sound?! You can fall into such a trap.
Pay attention to the phase characteristic. This happened with just one setting:
For any other Sampling rate and FFT size, the phase characteristic has a burst:
and the capacitance value is different, although the difference is 4%, the main thing is not to measure it at a phase jump. So, you see that there is food for thought and experimentation, maybe try to compare “singing” and “non-singing” capacitors. I tried connecting the windings of network transformers, and I got units and tens of Henry. Here is CCI 259.
Maybe it will be interesting for TV lovers to see Z of their transformers? I made a “short-circuited turn”, or rather short-circuited the low-voltage winding. Z dropped very significantly to 5 kHz, I don’t know what it will be like from one turn and whether it can be beneficial. I did all the measurements here using an attachment and an amplifier, as in the previous article on measuring Thiel-Small parameters, it was just more convenient for me, I don’t see any problems when taking measurements without an amplifier.
Acoustic measurements using Arta Software
The complexity of measuring the electrical and acoustic parameters of speakers often pushes one to abandon this procedure, and subsequently the process of creating speakers is carried out with a focus on simple calculation formulas that take into account only the electrical parameters of the speakers, and even then ideal ones. I think there is no point in going deeper into stories that the result in this case does not even come close to meeting expectations. I won’t lie, the measurement process is complicated, requires some special equipment and, very importantly, skills in working with programs for carrying out measurements. It’s not enough to just measure, you need to do it as objectively as possible, and the only limitation in measurements should be the error of the measuring equipment.
Next, I will try to talk in detail about the methodology for carrying out measurements in the Arta Software package. I fell in love with this program for its convenience and ease of use, and the ability to comprehensively analyze measurement results. The latest version of the program is available on the developers' website . At the moment this is version 1.6.1. There you can also download original manuals for working with the components of the package, although in English. These guides are included in the program's help system. You can call it through the menu Help – User Manual .
To take measurements you will need some equipment. Below is what I use:
1. DellInspiron 1720 laptop with WindowsXPProfessionalx86 operating system and ArtaSoftware software package installed.
2. Sound card E-MU 0404 USB.
3. Denon PMA-500AE amplifier. It is suitable because it has the function of bypassing tone correction, loudness and balance - Source Direct.
4. Voltmeter V7-38.
5. Resistance store P33.
6. Nady CM 100 measuring microphone.
7. Microphone stand. Its role is played by a camera stand, which has the functions of tilting, rotating and height adjustment.
8. “Reference” resistor (Rref), necessary for impedance measurements. I use PEV-10 with a nominal value of 10 ohms. The measured resistance is 9.85 ohms.
9. Two cables with dividers that protect the sound card input from dangerous voltage levels. The dividers are soldered inside the TRS jack.
10. XLR microphone cable and several cables for connecting the inputs/outputs of the sound card and connecting it to the amplifier.
First you need to read the article “Introducing and checking the measuring path with Arta Software”
To carry out acoustic measurements, it is possible to use two schemes: single-channel (Figure 27) and two-channel (Figure 28).
Figure
27
Figure
28
I strongly recommend working with a two-channel measurement scheme, but if you use the sound card's built-in preamplifier for a microphone connected to the Line In input, you will not be able to use a two-channel scheme. The single-channel method has a drawback - the reference position of the cursor is not defined in Arta. For some time I was forced to use a single-channel measurement scheme, so I had to look for a method for determining this position. Such a method was found. Perhaps it is not the best and not the most correct, but we could not find another method. I'll tell you about this in detail a little later. Now we connect the equipment in accordance with the selected measurement scheme and place a stand with a microphone in front of the speaker being measured. For complex measurements of speakers for a future acoustic system, the distance to the microphone should be set the same and the output voltage of the amplifier should not be changed during the measurement process. To measure speakers in the far field, in order to simplify the procedure for installing the microphone strictly on the axis of the RF emitter, I recommend using a laser pointer. As I write the material, I will take a near-field measurement (the distance between the microphone and the speaker is approximately 20 cm) of the 4A28 full-range speaker without acoustic design. Why do I not specify the exact voltage value at the amplifier output and do not adhere to a strict distance between the speaker and the microphone. It's simple. To measure absolute values of sound pressure, you need either a calibrated measuring microphone or an independent calibration procedure using a speaker for which there are measurement results obtained using a calibrated measuring system. The speaker sensitivity value calculated together with the other Thiel-Small parameters cannot be used as a standard. This value has too little in common with the real sensitivity of the speaker, and even more so with its frequency response. A specific voltage applied to the speaker should be adhered to when measuring the dependence of nonlinear distortion on frequency.
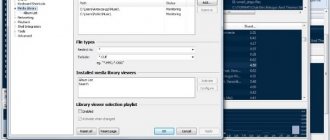
Launch Arta ( Start – All Programs – Arta Software – Arta ) . The familiar impulse response window will open (Figure 2). We check and, if necessary, adjust the settings in the Setup – Audio devices (Figure 3). Using a 400 Hz sinusoidal signal generator, accessible through the Setup – Calibrate devices (Figure 4), we set the required voltage at the amplifier output. We check the settings in the Setup – Analysis parameters (Figure 5). Go to the Record menu – Impulse response/Signal time record (Figure 6), open the Periodic Noise tab. This menu is partly already familiar. In the Sequence length field, the number of samples per period of the test signal is set, in the Sampling rate (Hz) field – the sampling frequency (Fs). In the Noise spectrum field, select the type of periodic noise signal: White, Pink and Speech. The Output volume field sets the test signal level. The Pink cutoff (Hz) field changes the cutoff frequency when using pink noise. On the right, in the Prefered input field, the measurement channel is selected. In this case, this is the channel to which the microphone is connected. In both measurement schemes (Figure 27 and Figure 28), the left channel is used as the measurement channel. Checking the Dual channel measurement mode box enables the dual channel measurement method. The Invert phase of input channel checkbox is used to change the phase of the input signal by 180 degrees. This is required if the speaker being measured is connected with reverse polarity. The Number of averages field indicates the number of measurements from which the impulse response will be calculated using the averaging method. When making acoustic measurements, I recommend setting the number of measurements to at least 10. This helps to reduce the measurement error due to less sensitivity to extraneous random noise. The Frequency domain 2Ch averaging checkbox is responsible for additional averaging in the two-channel measurement method, and the Filter dual channel impulse response checkbox is responsible for filtering in the Fs/2 frequency domain. On the Sweep tab of the Impulse response measurement window, the Log-frequency sweep checkbox allows you to select a change in the tone of the test signal according to a linear or logarithmic law, and the Generate voice activation checkbox enables the generation of a short tone burst before the test signal. The Center peak of impulse response checkbox is not available for two-channel measurements. It is responsible for the position of the pulse exactly in the middle of the test signal period. This is required when measuring the dependence of nonlinear distortions on frequency. Checking the Close after recording checkbox, available when opening any tab, will ensure that the Impulse response measurement window is closed upon completion of the measurement process.
Since with two-channel measurements it is possible to automatically calculate the delay value, I will begin the description with the single-channel measurement method. I’ll tell you a little later what actions need to be performed during two-channel measurements.
Go to the Periodic Noise tab of the Impulse response measurement menu and make the required settings. I installed these (Figure 29):
Figure
29
Turn on the noise generator by pressing the Generate button and adjusting the sensitivity to set the input signal level in the range of -20...-10 dB. Let me remind you that only the left channel, to which the microphone is connected, is used. Once the installation is complete, turn off the generator by pressing the Generate button again. Now we start measurements by pressing the Record button. After completing the measurement process, we return to the impulse response window (automatically or independently).
Now is the time to talk in more detail about the main disadvantage of single-channel measurements - the uncertain reference position of the cursor. On the one hand, there are no problems - we place the cursor in front of the pulse, and the marker at the maximum of the pulse and we get a delay for calculating the phase response. This is true, but incorrect cursor placement is clearly visible on the Cumulative Spectral Decay graph. It is with this that we will determine the reference position of the cursor. How correct this method is can be concluded later based on the results of measurements using the two-channel method. So, look at the resulting impulse response graph (Figure 30).
Figure30
Now the cursor is set to position 0 ms (0 samples), so we leave it there. We place the marker immediately after the impulse. I set it to 4.646 ms. To avoid early reflections in the signal, do not place the marker too far away. The optimal time window is 4…5 ms. Click the button with the letters CS on the toolbar or select Analysis – Cumulative spectrum . The Cumulative Spectrum Setup window opens (Figure 31). This graph is abbreviated as CSD (Cumulative Spectral Decay).
Figure
31
The Log frequency axis checkbox is checked if a logarithmic scale of the frequency range is required. The Remove antialiasing range checkbox enables filtering of frequency range components in the Fs/2 area. dB range (10 – 70) and Maximum frequency (Hz) set the on-screen dynamic range and top frequency respectively. The Smoothing field sets smoothing, and the Use FR compensation checkbox enables the frequency response compensation set in the Setup – FR compensation (for obvious reasons, I did not talk about this menu). On the right side of the window, the top field switches the analysis type. When working with impulse response, the type is automatically set to Analyze as CSD using apodizing window. The FFT length (in samples) field sets the number of samples in the FFT block. If the length of the time window in samples is less than FFT lenght/2, the program will display a warning when starting the analysis. The FFT block shift (in samples) field indicates the duration of the timeline in samples, and the Max. number of FFT blocks – number of FFT blocks included in the timeline. The Apodizing window rise time (0.02-1ms) field specifies the opening and closing time of the analysis window. The value of 0.2 ms is a certain optimum when analyzing characteristics in both the low and high frequency regions. Make the settings and click OK.
If a pattern similar to that shown in Figure 32 is observed, it is necessary to increase the time scale (FFT block shift).
Figure
32
When using the correct CSD settings, the graph should look similar to (Figure 33).
Figure 33
The graph shows the presence of FFT blocks with the same content. This is a consequence of incorrect placement of the cursor in the impulse response window - the cursor position is too early in relation to the impulse. If you place the cursor in a position that “cuts off” the useful data, the analysis of the resonant processes themselves will take place in the CSD window, without the signal generating them. This will also be reflected in the frequency response graph. Since the time scale is not very conveniently expressed on the Waterfall chart, I suggest switching to a sonogram - in the Mode field, select Sonogram (Figure 34).
Figure 34
Here's a more visual timeline. To improve the resolution, I check the Grid box and set the CSD settings to a smaller time scale. We changed the settings and display the graph (Figure 35).
Figure
3 5
It can be seen that the signal spectrum does not change until approximately 2.74 ms. This is the desired cursor position. We close the window.
In the impulse response window, set the cursor to the position 2.74 ms (near this value), and the marker to the maximum impulse, thereby obtaining the delay value (Figure 36).
Figure
36
Here I will make a small digression regarding the maximum momentum. As you can see above, the position of the maximum impulse can be taken differently if you “expand” the impulse response by 180 degrees. In this case, the maximum of the impulse will be a little further in time. This is an incorrect setting and will certainly affect the phase response. To make sure that the impulse response has a “positive” response, we will use the step response graph. Click on the button labeled STEP on the toolbar, or select Analysis – Step response . The Step response window opens (Figure 37).
Figure
37
As you can see, the transient response has a “positive” edge. If the transient response has a “negative” edge (Figure 38), then it is necessary to change the phase of the impulse response in the impulse response window using the Inv button located on the toolbar (or through the Edit – Invert ). You can re-measure by changing the polarity of the speaker connection, or re-measure with the Invert phase of input channel checked in the Impulse response measurement window.
Figure
38
Returning to the impulse response window. We set the cursor, marker and got the delay value. Now use the marker to set the measurement window (Gate) to about 4...5 ms (Figure 39).
Figure
39
Open the CSD window, make the settings and look at the result (Figure 40).
Figure40
You can make sure that the CSD graph is displayed correctly by looking at the frequency response graph (Figure 41).
Figure41
We return to the impulse response window. The cursor has been installed, the delay has been calculated, and now you can select the marker position, thereby determining the measurement window and the lower limit frequency when analyzing the characteristics. Now I have a near-field measurement, so I can set the measurement window to be long - about 50 ms - and get a lower cutoff frequency of 20 Hz in the analysis. But when measurements are made in the far field, or the room has unsatisfactory acoustic properties, it is advisable to limit the measurement window even before the arrival of the first reflections. I will show how to recognize them in the impulse response window using the example of a measurement result of an RF emitter in the far field (Figure 42).
Figure
42
In Figure 42, the cursor is positioned at the position that displays the boundary of the pure impulse response. The cursor is followed by reflections - early and late. Early reflections are very clearly visible as a pulse repeated three times. Late reflections have a significantly larger amplitude, in rare cases even comparable to the amplitude of the main impulse response.
So, we define the measurement window. I set it to 56.594 ms (5433 samples). Now you can proceed to analyzing the measurement results and exporting them to a format supported by CAD systems. The impulse response can be saved in Arta format (*.pir), or exported to text format. The following graphs are available for analysis: frequency response, phase response, group delay, phase change, pulse energy versus time graph, cumulative spectrum attenuation and decay graph. For frequency response, phase response and group delay graphs, there are additional menus that allow you to view graphs without smoothing and a menu with the ability to build graphs using two time windows.
The button with the letters FR, located on the toolbar, opens the Smoothed frequency response menu (via the menu – Analysis – Single-gated smoothed Frequency response/Spectrum ) – Figure 43.
Figure
43
At the bottom left are the Mag, M+P, Ph and Gd buttons. With their help, the graphs of the frequency response, frequency response + phase response, phase response and group delay are opened, respectively. On the right, in the Smoothing field, select a smoothing characteristic from the list. Right-clicking on the graph opens an OSD menu where you can set the dynamic and frequency ranges of the measurements. In the File – Export… , you can export measurement results to text format. Overlay menu controls curve layers. You can “pin” a curve to a graph to create a combined graph. For example, to compare the frequency response on the main axis and with deviation from the axis (Figure 44).
Figure
44
Using the Edit – Scale level , the curves are normalized (in the graph above, the curves are first normalized at a frequency of 100 Hz and only then combined). LF box diffraction menu is used to compensate for the so-called “baffle”. The phase characteristic can be displayed as the minimum phase ( Minimum phase ), excess phase ( Excess phase ) or measured phase (the checkboxes for the minimum and excess phase are unchecked). Activating the Unwrap Phase disables the phase “flip” on the phase response graph when the value reaches -180 or 180 degrees. The group delay can be calculated from the excess phase ( Excess group delay is activated) or from the measured phase ( Excess group delay is not checked).
Graphs of frequency response, phase response and group delay can be displayed using a combined method with two time windows ( Analysis – Dual-gated smoothed frequency response or the button with the letters 2FR on the toolbar). To do this, in the Setup – Analysis parameters (Figure 5) in the Gate1 and Gate2 fields, you must specify the duration of each window. In the Gate1 field it is possible to set values from the range 5…60 ms, and in the Gate2 field – 70…300 ms.
menu – Unsmoothed DFT frequency response/Spectrum or clicking the button with the letters DFT on the toolbar allows you to view graphs of the frequency response, phase response and group delay without smoothing (Figure 45).
Figure
45
The decay plot (in the Analysis – Burst decay or the BD button on the toolbar) looks very similar to the CSD plot. Their difference lies in the method of analysis. Arta Software developers recommend analyzing both graphs. In general, the presence of resonances is clearly visible from the cumulative spectrum graph, but it is the pronounced resonances that are more clearly displayed on the Burst Decay graph (Figure 46 and Figure 47).
Figure
46
Figure
47
To assess the nonlinear distortions of the speaker, you can measure the dependence of the level of nonlinear distortions on frequency (menu Analysis – Frequency response and distortions ). To do this, first go to the Setup – Analysis parameters and in the FFT length field select the value 131072. In the Impulse response measurement window, go to the Sweep tab. If the two-channel measurement method is used, disable it and check the Center peak of impulse response checkbox. In the Sequence length field, select the value 128k. We start the measurement process. For example, below (Figure 48) shows a graph of nonlinear distortions of a 4A28 wideband speaker with an input power of 1 W (3.464 v at a load of 12 Ohms).
Figure48
The graph does not display the total level of distortion, but separately the harmonics. If you need to know THD, you will have to independently convert decibels to percentages and calculate harmonic distortion. Just out of curiosity, I did this procedure and got the following results. THD at a frequency of 100 Hz is 1.5347%, at a frequency of 1 kHz – 1.9369%, at 10 kHz – 2.1475%.
Now about two-channel measurements. We connect the equipment according to the diagram in Figure 28. In the Setup – Calibrate devices (Figure 4) menu we set the voltage at the amplifier output, and in the Record – Impulse response/Signal time record (Figure 6) menu on the Periodic Noise tab we set the input signal levels in the range -20…-10 dB. For two-channel measurements, Arta can independently determine the delay for phase calculation. I use automatic calculation only if it is impossible to determine the position of the maximum impulse in the impulse response window. This happens when measuring a woofer with a low-pass filter connected. The delay is determined in another Arta window – Dual channel – frequency response. To switch to it, you must select Dual channel – frequency response Mode or press the button with the letters Fr2 on the toolbar. The Impulse response window will change (Figure 49).
Figure
49
The settings menus are slightly different from those available when working in the impulse response window. Some fields are used to configure the program when working with a spectrum analyzer, so I will skip these fields in the description.
Go to the Setup – Measurement (Figure 50).
Figure50
In the FFT size field we indicate the FFT block size – 16384, in the Sampling rate field – the sampling frequency. Check the Phase box, and in the Prefered input channel field select the channel to which the microphone is connected. In the Propagation delay field, be sure to set the value to 0. OK.
On the toolbar, in the Gen field, set the value to PN pink and take the measurement (Figure 51).
Figure51
The phase characteristic, due to the lack of a delay value, is displayed with an error. Automatic delay determination is performed through the Record – Crosscorrelation/delay estimation (Figure 52).
Figure52
The Delay(ms) field displays the delay value. To use this value, simply click the Accept button. There is a return to window Fr2, where the delay value is automatically entered in the Delay (ms) field. We take the measurement again (Figure 53).
Figure53
Now the phase response is measured correctly. We remember the delay value specified in the Delay(ms) field in the clipboard and go to the impulse response window (Imp button on the toolbar or in the Mode menu – Impulse response/Signal time record ). When switching, the program will offer to convert the Fr2 measurement result into an impulse response (Figure 54).
Figure54
You can agree, you can refuse. This is unimportant, since during conversion the position defined as the reference for the cursor in two-channel measurements is violated. Therefore, the measurement must be carried out again, but this time through the Record – Impulse response/Signal time record (Figure 6). We set up the fields for the two-channel method and take measurements. In the impulse response window, the reference cursor position for two-channel measurements is precisely defined - 300 samples. We place the cursor in this position, in the Delay for phase estimation (ms) field we set the value of the delay obtained during measurements in Fr2. It remains to set the length of the measurement window and you can begin analysis and export (Figure 55).
Figure55
For comparison, Figure 56 and Figure 57 show CSD graphs when measured using the single-channel and dual-channel methods, respectively. In the graph Figure 58, the phase response response is shown in blue when measured using a two-channel method, and in red when measured using a single-channel method.
Figure56
Figure
57
Figure58
I hope the material I have presented will help in working with the program. It in no way replaces the original reference manuals, which I recommend that anyone who will use the program study. These manuals contain answers to 99% of questions that arise when using Arta Software.