We carry out calculations and installation of Helmholtz Resonators, more than 30 direct flows have already been saved. We carry out measurements and calculations ourselves, and we guarantee our work.
Helmholtz resonance
- the phenomenon of air resonance in a cavity, an example of which is the hum of an empty bottle from an air flow directed perpendicular to its neck.
A Helmholtz resonator
is a spherical copper vessel with an open neck, invented by Helmholtz around 1850 to analyze acoustic signals; based on the phenomena observed in it, Helmholtz and Rayleigh developed a quantitative theory of resonance of this type
Acoustic resonator, Helmholtz resonator
Acoustic resonator, Helmholtz resonator
- a vessel communicating with the external environment through a small hole or pipe (throat). A characteristic feature of an acoustic resonator is that the wavelength of its own low-frequency oscillations is much larger than the dimensions of the acoustic resonator.
For an acoustic resonator with a throat, the natural frequency is , where c is the speed of sound in air, S is the cross-sectional area, l is the length of the tube, V is the volume of the vessel. If an acoustic resonator is placed in a harmonic sound field with a frequency f, oscillations arise in it with an amplitude many times greater than the amplitude of the field (resonance). In a non-harmonic sound field, the acoustic resonator responds only to vibrations with frequency f. Therefore, a set of acoustic resonators with different natural frequencies can be used for sound analysis. If there is friction in the throat of an acoustic resonator, strong absorption of sound at frequency f occurs in it, which is used to create the so-called. resonant sound absorbers in architectural acoustics. Acoustic resonators placed on the walls of sound ducts serve as elements of resonant reflectors to reduce the transmission of low-frequency noise along sound ducts. Bubbles in liquids and air spaces in certain other media (for example, rubber) are also acoustic resonators, so the presence of a large number of bubbles in water causes strong sound absorption, which prevents the propagation of sound waves.
The theory of acoustic resonators was developed by G. Helmholtz (1860).
to the library to the table of contents FAQ on ethereal physics TOEE CHPP TPOI TI
Did you know,
that, like any idolatrous religion, relativism is a tool for the ideological subordination of some people to others through the absolutely unscrupulous manipulation of their psyche to achieve the interests of certain groups of people at the helm of this thieving machine? Read more in the FAQ on ethereal physics.
| FORUM NEWSKnights of the theory of ether | 01.10.2019 - 05:20: EDUCATION, ENLIGHTENMENT, EDUCATION - Upbringing, Inlightening, Education -> - Karim_Khaidarov.30.09.2019 - 12:51: EDUCATION, ENLIGHTENMENT, EDUCATION - Upbringing, Inlightening, Education -> - Karim_Khaidarov.30.09. 2019 - 11:53: EDUCATION, ENLIGHTENMENT, EDUCATION - Upbringing, Inlightening, Education -> - Karim_Khaidarov.09.29.2019 - 19:30: CONSCIENCE - Conscience -> - Karim_Khaidarov.09.29.2019 - 09:21: ECONOMY AND FINANCE - Economy and Finances -> - Karim_Khaidarov.09.29.2019 - 07:41: EDUCATION, EDUCATION - Upbringing, Inlightening, Education -> - Karim_Khaidarov.09.26.2019 - 17:35: EDUCATION, EDUCATION - Upbringing, Inlightening, Education -> - Karim_Khaidarov.09.26.2019 - 16:35: WAR, POLITICS AND SCIENCE - War, Politics and Science -> - Karim_Khaidarov.09.26.2019 - 08:33: EDUCATION, EDUCATION - Upbringing, Inlightening, Education - > - Karim_Khaydarov.09.26.2019 - 06:29: EDUCATION, EDUCATION - Upbringing, Inlightening, Education -> - Karim_Khaydarov.09.24.2019 - 03:34: THEORETING AND MATHEMATICAL MODELING - Theorizing and Mathematical Design -> - Karim_H Aidarov. 09.24.2019 - 03:32: NEW TECHNOLOGIES - New Technologies -> - Karim_Khaidarov. |
Application
Helmholtz resonance is used in internal combustion engines and in acoustic systems. Fuel injection systems called Helmholtz systems
used in the Chrysler V10 engines found in Dodge Vipers and Ram pickups, as well as in Buell motorcycles. In hollow-back string instruments, such as a guitar or violin, one of the peaks of the resonance curve is the Helmholtz resonance (the others are the resonant frequencies of the wood of the instrument). Ocarina is a resonator with a variable neck section. The West African djembe drum has a relatively narrow neck, which gives it a deep bass tone.
Helmholtz resonance theory is used in the design of automobile and motorcycle exhaust pipes to make the engine sound quieter or more beautiful.
Resonators and soundboards
Table of contents
| Acoustics of the vocal apparatus |
| Origin and propagation of sound |
| Tone and noise sounds |
| Pitch |
| Behavior of waves when encountering obstacles |
| The power of sound |
| Sound timbre |
| Resonance phenomenon |
| Resonators and soundboards |
| Sound of the glottis |
| Formants |
| The role of the nasal resonator |
| Vibrato |
| Sound emission |
| The vocal apparatus is a kind of mouthpiece |
| Radiation direction |
| Interconnected system |
| Flight of the singing voice |
In acoustics, a resonator means any volume of air enclosed in elastic walls and having an outlet. It is called a resonator because if the air in it is excited to vibrate, the resonator will produce a sound of a very specific pitch. Helmholtz resonators are built on this principle. The pitch of sound that is generated in the resonator depends on the volume of air contained in it, the shape of the resonator and the size of the outlet hole. This tone is called the resonator's own tone. From an acoustics point of view, a glass, a hollow ball, a tube, a bottle are resonators. The smaller the size of the resonator and, at the same time, the volume of air contained in it, the higher the tone that is born in the resonator - its own tone. The smaller the output hole, the lower the natural tone. This phenomenon is based on the formation of a so-called standing wave, which “runs” in the walls of the resonator from its bottom to the edge and back. Since the speed of propagation of the wave in the air is constant, then during the same time in a small volume of air the wave will have time to make many complete oscillations (i.e., its own tone will have a high frequency), and in large volumes - few (i.e., a low frequency ). This explains the phenomenon that the natural tone of resonators of small magnitude is high, and of large magnitude is low. The structure of organs is based on the phenomenon of natural vibrations that occur in pipes, where the lowest sounds occur in pipes several meters long, and the highest - 1-2 cm. When we pour water from a tap into a bottle, we hear the sound As it fills with water, it becomes higher and higher, resembling a whistle when the water reaches the neck. This is due to a decrease in the column of oscillating air, and the source of oscillations is its shaking by a falling stream of water. Resonance phenomena in resonators arise according to the same principle as in strings. The resonator “responds,” i.e., it produces air vibration when a sound is emitted above it that matches the frequency (pitch) of its own tone. Since in this case the natural frequency of the resonator coincides with the frequency of the waves approaching it, each new wave pushes its own wave “running” in the resonator in time, as a result of which the buildup becomes greater and greater. Energy accumulates. The resonator begins to “sound out.” It also echoes the overtones of its own tone, but only less strongly. If the frequency of the waves approaching the resonator does not coincide with the natural oscillations that arise in the resonator - with its own tone, swinging will not work (just as a swing does not swing if it is not pushed in time). As with string resonance, the resonator itself does not add energy, but only accumulates and accumulates the energy contained in the waves approaching it. Then the resonator transmits it to the outside environment, hums, and resounds, causing the sound to become louder for the listener. Rice. 17. In the human vocal apparatus there are many cavities and tubes in which resonance phenomena can develop. The trachea and bronchi, the cavity of the larynx, pharynx, mouth, nasopharynx, nose and the small adnexal cavities surrounding it have sufficiently elastic walls for resonance phenomena to occur in them. Some of them are unchangeable in shape and size, given by nature, therefore they always enhance the same overtones, generate overtones that are constantly present in the voice and cannot be specially adapted to enhance any other overtones (for example, the nose and its subordinates cavities). Others easily change their shape and size, for example, the oral cavity, pharynx, and supraglottic cavity of the larynx, i.e., they can be used within a wide range to change the original timbre by resonator amplification of certain groups of overtones. It is thanks to resonator phenomena in the spectrum of a person’s voice that “peaks” are obtained, intensifications of individual overtones, which are often stronger than the fundamental tone. In stringed instruments, the main mechanism that changes the original timbre of the strings is the soundboard. Soundboards are understood as specially constructed wooden boards that form, for example, in violin instruments, their body. The soundboards give off to the air the vibrations that they received from the source of vibrations - from the strings. However, they are not only transmitters, but also transformers of the timbre of the original string sound. In order to understand how this happens, we allow ourselves to give the following example. Everyone! The xylophone is known - an instrument consisting of individual wooden planks - blocks of various lengths, which, when struck with a stick, emit a musical tone of a certain pitch. This tone depends on the length of the block, its thickness and the material from which it is made. Accordingly, the board will resonate to this tone. Decks can be thought of as a sum of such planks, fastened together and having different shapes for different instruments. The sound from the vibrating string, having the appearance of a decreasing palisade of amplitudes, is transmitted to the soundboards. The latter begin to vibrate with their own inherent vibrations, as a result of which not so much the spectrum that is generated by the string is emitted into space, but rather the spectrum that is characteristic of the soundboards and instrument bodies. It is well known that the value of a violin is determined by the structural features of its body and its soundboards, and not by the quality of the strings stretched on it. The same applies to the piano, where, in addition to mechanics, what is valued above all is what gives a beautiful sound, i.e. the quality of wooden structures, soundboards. As a result of soundboard vibrations, certain overtones that resonate well in the soundboards may turn out to be relatively stronger than others. Thus, from a decreasing palisade of frequencies, characteristic of string vibrations, a spectrum is formed with individual amplifications, as they say “peaks,” of certain frequencies. There are no such decks in the voice apparatus. The mechanism for changing the original timbre, born in the glottis, is not associated with vibrations of the chest, palatine vault or any other parts of the body, as is sometimes written about in old manuals. The change in the initial timbre of the larynx depends entirely on resonator phenomena developing in the cavities of the vocal apparatus. Currently, both the sound arising in the glottis and the effect of resonator cavities on it have been studied.
Qualitative explanation
When air is forced into a cavity, the pressure in the cavity increases. When the external force forcing air into the cavity disappears, the increased pressure causes the air to flow back out. After some time, the pressure inside and outside will be equal, but the air will still continue to flow out, since the stream of air in the neck has mass and non-zero speed, and therefore kinetic energy. After some time, air will stop leaving the cavity, and the pressure inside the cavity will be less than the pressure outside. The air will rush into the cavity again. This cycle will be repeated many times, with a decaying amplitude. The cycle frequency (natural or resonant frequency) depends on the shape of the cavity. If an external force appears and disappears with a frequency equal to the natural frequency of the cavity, a resonance will arise - air vibrations will not dampen.
What is a resonator
A resonator is an oscillation amplifier, and the phenomenon of acoustic resonance is that one acoustic system vibrates when another sound system sounds next to it with an oscillation frequency that coincides with the oscillation frequency of the first:
- A resonator can be a stretched string, an open or closed volume, for example, in the form of a wooden, metal or glass cylinder (tube), a plate attached to something at one end, or a tuning fork, etc.
- Oscillations are excited inside the resonator by even weak sound waves incident on it.
- How does a resonator increase the intensity of vibrations entering it?
There are two answers:
- Or the resonator absorbs energy scattered in space
- Either the waves intensify due to a decrease in the duration of the oscillations
- And both answers are equally valid
- For example, in the theaters of Ancient Rome, so-called “harmonicas” were specially installed - these are open volumes, and their neck was connected to the surrounding air space
- The air mass in the neck is set into oscillatory motion under external sound pressure
- And the resonant frequency is determined by this mass, plus the flexibility (compressibility) of the air volume in the resonator
- The oscillation speed at resonance in the throat of the resonator increases, and the volumetric flow also increases
- And due to the fact that the oscillation speed of the incident wave remains constant, while maintaining an increasing flow, the front of the incident wave is deformed
- Then the deformation covers a larger zone, the higher the vibration speed in the neck
- That is why the resonator concentrates much more energy contained in the part of the wave entering it, which falls on the area of its entrance hole
- Then the resonator releases all the accumulated energy, after the external influence on it ceases, into the space surrounding it
| Astronet | Picture of the day | astro-ph Reviews | News | Articles | Books | Sky Map | Constellations | Variable Stars | A&ATr | Glossary |
| planet Astronet | Physics of space | Biographies | Dictionary | Keywords | Astronomy in Russia | Forums | Seminars | Supernovae |
Oscillations and waves. Lectures.
V.A. Aleshkevich, L.G. Dedenko, V.A. Karavaev (Physics Faculty of Moscow State University) Publishing House of the Physics Faculty of Moscow State University, 2001 Contents
In Fig. Figure 5.12 is a “hearing diagram” that shows the ranges of frequencies and sound pressures, as well as the intensity levels of sounds perceived by the human ear. The normal ear hears only those sounds that lie within this area. The lower boundary of the region characterizes the dependence of the hearing threshold on frequency, and the upper limit characterizes the threshold of pain when the wave is no longer perceived as sound, causing a sensation of pain and pressure in the ear. Note that the human ear is a unique receiver of acoustic waves, perceiving sounds that differ in intensity by 12-15 orders of magnitude in the frequency range of about 1 kHz, where the hearing diagram has the largest vertical section. The diagram shows that with the same sound pressure and the same intensity, sounds of different frequencies can be perceived as sounds of different volumes. Therefore, in acoustics, in addition to the subjective value - the loudness of the sound assessed by ear, objective characteristics of sound are also used that can be directly measured - the level sound pressure and an equal intensity level. Since according to (5.17) the intensity is proportional to the square of the sound pressure, both of these characteristics are determined by the formula:
| (5.30) |
| Rice. 5.12. |
In principle, it is a dimensionless quantity, but for the numerical value of the logarithm the name “Bel” is used (in honor of the inventor of the telephone, G. Bell). In practice, a unit that is 10 times smaller, the “decibel,” is usually used, so (5.30) takes the form:
| (5.30a) |
In the definition, it is customary to use the standard hearing threshold and the corresponding value of the minimum intensity depends, according to (5.17), on the medium in which the sound propagates, and for air under normal conditions it is
For sound volume, a unit called “phon” is used. The volume of a tone in the backgrounds for any frequency is equal to the sound pressure level in decibels for a tone with a frequency perceived as sound of the same volume.
In Fig. 5.12 also shows curves for levels of equal loudness at different levels of sound pressure and intensity, from which it can be seen that for other frequencies audible to the ear and can differ noticeably.
Acoustic resonators.
In some cases, it becomes necessary to isolate harmonic components from complex sound vibrations. This problem has to be encountered in the above-mentioned spectral analysis of complex sounds, in the creation of narrow-band sound receivers sensitive to a certain frequency, musical instruments, etc. For such purposes, an acoustic resonator is used - a device with one or many natural frequencies.
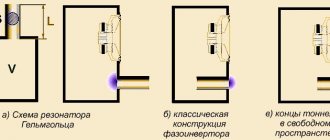
A typical example of an acoustic system that responds to only one frequency is a spherical vessel with an open neck (Fig. 5.13), which is called a Helmholtz resonator
. At the back of the resonator there is another small hole in the form of a nozzle, which serves to detect vibrations. The air in the throat is an oscillating mass. When this mass is displaced, for example, towards a spherical volume, the air in this volume is slightly compressed, and the resulting excess pressure forces act as a restoring force. If the area of the neck is equal to and its length is equal to, then the mass of the oscillating column is equal to where is the density of undisturbed air. When the mass is displaced by a distance (the positive direction of the axis is shown in the figure), the air density changes by a value satisfying the equality
| (5.31) |
According to (5.7), the excess pressure turns out to be equal
| (5.32) |
Consequently, the equation of motion of the air column takes the form
or
| (5.33) |
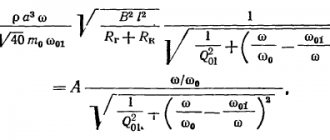
From here we find that the natural frequency of oscillation of the air column in the neck, or the frequency of the Helmholtz resonator, is equal to
| (5.34) |
Given the volume of the resonator, the area of the neck opening and its length, the speed of sound for the frequency we obtain the value
| (5.35) |
corresponding to the audible range of sound frequencies.
| Rice. 5.13. |
The dependence of the natural frequency of the resonator on its parameters and, above all, on the volume is effectively demonstrated in the following experiment (Fig. 5.14). Several resonators differing in size are installed in front of the speaker D, connected to the audio frequency generator D. A lightweight paper propeller-turntable is placed near the rear hole of each of the resonators, which can rotate around a vertical axis. With a gradual increase in the frequency of the sound generator, the frequency of the acoustic wave emitted by the speaker in the direction of the resonators and playing the role of a harmonic driving force will increase. When the frequency of this wave consistently coincides with the natural frequencies of the resonators, the air pressure in their volumes will fluctuate with a maximum (resonant) amplitude. Strong jets of air will erupt from the rear holes of the resonators, which is detected by the start of rotation of the turntables, first at the large one, then at the middle one, and finally at the smallest resonator, which has the highest natural frequency
| Rice. 5.14. |
It is appropriate to note that at the frequency of the resonator, the length of the wave that excites it is much greater than the characteristic dimensions of the resonator: Consequently, there can be no talk of a standing acoustic wave of frequency in the spherical cavity itself.
However, in the cavity itself it is possible to excite standing waves with a length and frequency If the characteristic size of the resonator is the frequency of these waves. Such a resonator will have many natural frequencies in the kilohertz range.
The easiest acoustic resonator to manufacture is a wooden box or pipe, open on either one or two opposite sides.
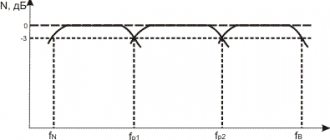
Let's do the following experiment. Let's fill the lower part of the vertical tube T with water, using a system of communicating vessels, and bring a tuning fork K sounding at the frequency to the upper end (Fig. 5.15). By moving funnel B up, you can enhance the tonal sound created by the “tuning fork + part of the pipe filled with air” system. This amplification will occur when the frequency coincides with one of the natural frequencies of the resonator - a pipe with air with a length “closed” at the lower end. The natural frequencies of standing waves in such a resonator are easy to calculate, given that there should be a displacement node at the lower end, and an antinode at the upper end. This is possible only for wavelengths that satisfy the condition (4.40) stated in the previous lecture:
when there is an odd number of quarter wavelengths along the length of the pipe. Accordingly, the oscillation frequencies will be equal
| (5.36) |
Although sound amplification will occur at several lengths of the air column, it will be most effective at or
| Rice. 5.15. |
We especially emphasize that the resonator creates more favorable conditions for the sound of a tuning fork, allowing it to be redistributed, and therefore amplified, in certain directions. That is why in experiments tuning forks are installed on a wooden box, open at one end and tuned to the frequency of the tuning fork (Fig. 5.16).
| Rice. 5-16. |
Back| Forward
| Publications with keywords: oscillations - waves Publications with words: oscillations - waves | |
See also:
| |
Discuss this post
print version
Astrometry
—
Astronomical instruments
—
Astronomical education
—
Astrophysics
—
History of astronomy
—
Cosmonautics, space exploration
—
Amateur astronomy
—
Planets and the Solar System
—
The Sun
Sound waves and their properties
Sound wave (sound) - this is how we usually call waves that are perceived by the human ear:
- The range of so-called “sound” frequencies is within
- approximately 20Hz to 20kHz
- Waves with a frequency below 20 Hz are called infrasound, and those above 20 kHz are called ultrasound.
- Waves from the sound range easily propagate not only through gases (air), but also through any liquids (the so-called longitudinal waves) and even in solids (these are longitudinal and also transverse waves)
- However, waves propagating in a gaseous medium - the main medium of interest to us - are of particular interest
A special branch of physics studies sound phenomena, which is best familiarized with before making a subwoofer with your own hands, called acoustics:
- When a sound wave propagates in a gas, both molecules and atoms oscillate along the propagation of the wave, which leads to changes in the local density of the gas and its pressure
- Therefore, sound waves in gas (air) are often called density waves or pressure waves
- The human ear, picking up various sounds, first of all evaluates them according to the degree of loudness, which depends on the intensity of the wave
- And the effect of sound waves on the eardrums depends on its sound pressure, the amplitude of pressure fluctuations in the wave itself
- The human ear is the most perfect receiver created by Nature itself, which is capable of perceiving sounds in a very wide range of sounds: from the squeak of a mosquito to the roar of an erupting volcano.
- Thus, our ear is able to perceive even waves whose sound pressure changes millions of times
- The sound intensity is proportional to the square of the sound pressure, and the intensity range is about 1012, incredible!
- Such a huge range of audibility of the human ear corresponds to the use of a device capable of measuring both the diameter of an atom and the size of a football field
- For example, let's say that when people talk in a room, the emitted sound intensity is approximately 106 times higher than the threshold of its audibility, and the sound intensity at rock concerts is often close to the pain threshold
- Another characteristic of a sound wave that determines its auditory perception is the so-called “height” of the sound.
- Vibrations of a “harmonic” sound wave are perceived by the human ear as musical tones
- High-frequency vibrations are perceived by us as high-pitched sounds, and low-frequency vibrations are perceived as low-pitched sounds.
- The sound produced by musical instruments and the sounds of human voices can vary significantly in frequency range and pitch
- For example, the range of the lowest timbre of a male voice, bass, extends from 80 Hz to 400 Hz, and the range of the highest timbre of a female voice, soprano, extends from 250 Hz to 1050 Hz.
- The singer's larynx works as an acoustic resonator
- How to connect acoustics in a car is a completely different article, this one is about resonators